数学(24分)

要拿到（80%）20分以上。

• 学习方法（数学+理论力学+材料力学+流体力学）
• 向量代数与空间解析几何（2分）
  • 向量及其运算（1分）
  • 空间平面
  • 空间直线
  • 直线与平面的位置关系
  • 空间曲面、曲线
  • 常用函数图像
• 函数极限连续（2分）
  • 函数的概念及性质
  • 极限的概念及计算（1分）
  • 无穷小的比较
  • 连续
  • 间断点
  • 渐近线
• 导数与微分（6分）
  • 导数的概念及定义计算（0.6分）
  • 一元函数导数及微分（1.4分）
  • 多元函数偏导数及全微分（2分）
  • 导数的应用（2分）
• 积分学（4分）
  • 不定积分计算（1分）
  • 定积分计算（1.3分）
  • 一次定积分应用（0.3分）
  • 二重定积分计算（1分）
  • 曲线积分（1分）
• 微分方程（2分）
  • 微分方程基本概念（0.1分）
  • 一阶线性微分方程（0.8分）
  • 二阶微分方程（1分）
  • 线性微分方程解的结构（0.1分）
• 无穷级数（2分）
  • 常数项无穷级数（1分）
  • 幂级数收敛性
  • 和函数
  • 函数展开幂级数
• 线性代数（3分）
  • 矩阵的运算与性质（1分）
  • 线性方程组（0.6分）
  • 向量组的线性相关性（0.6分）
  • 方阵的特征值与特征向量（0.6分）
  • 二次型（0.6分）
• 概率论与数理统计（3分）
  • 事件的关系和运算（1分）
  • 分布函数（列）、概率密度函数（0.8分）
  • 数学期望和方差（0.8分）
  • 正态分布（0.2分）
  • 参数估计（0.4分）

学习方法（数学+理论力学+材料力学+流体力学）

1. 以教程和课件为基础，理解+记忆
2. 重点反复做历年考试真题(分类真题|年份真题)——务必动手写过程
3. 真题以外，只做我提供的练习题

向量代数与空间解析几何（2分）

难度低，易拿分，全拿。

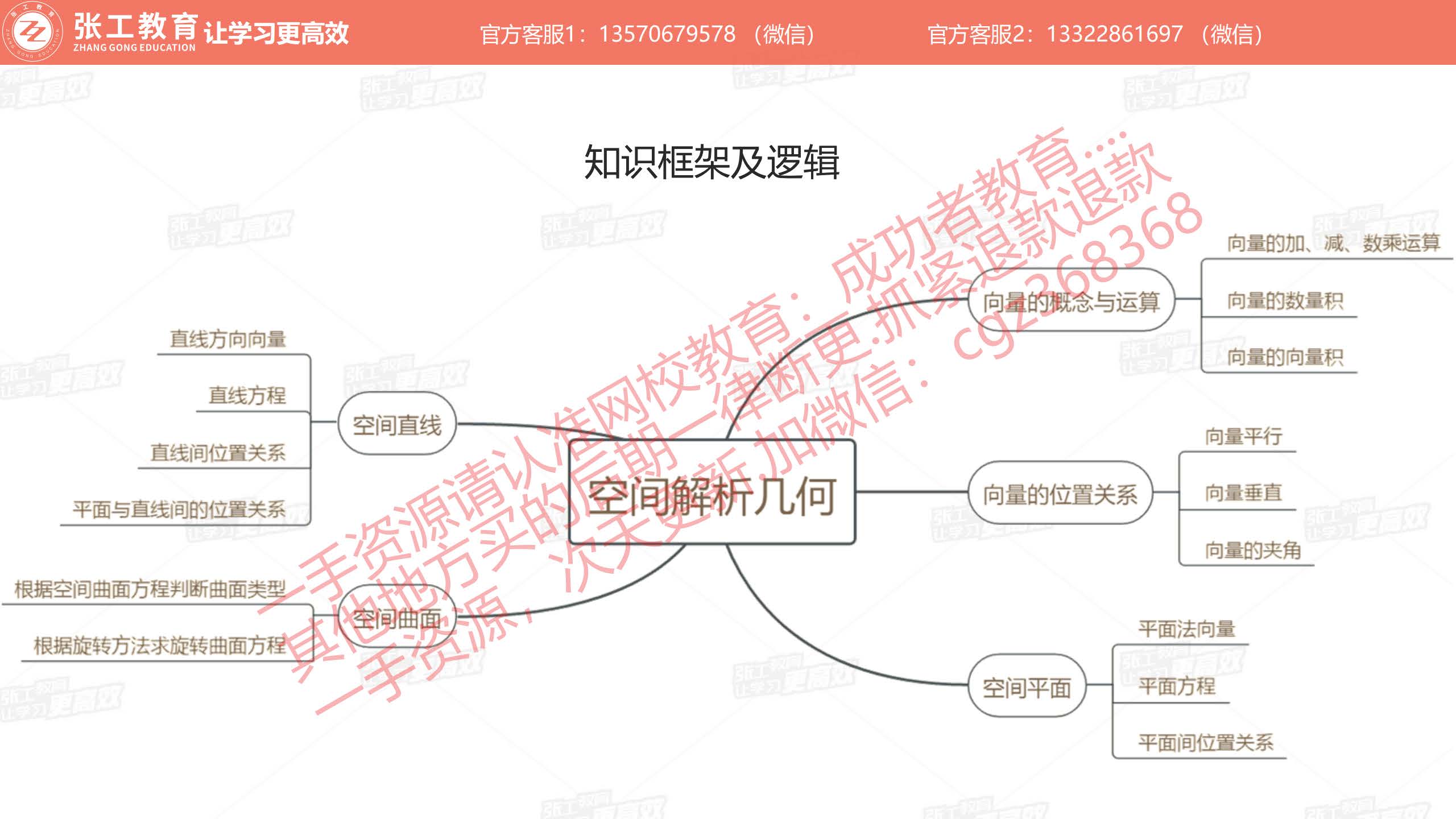
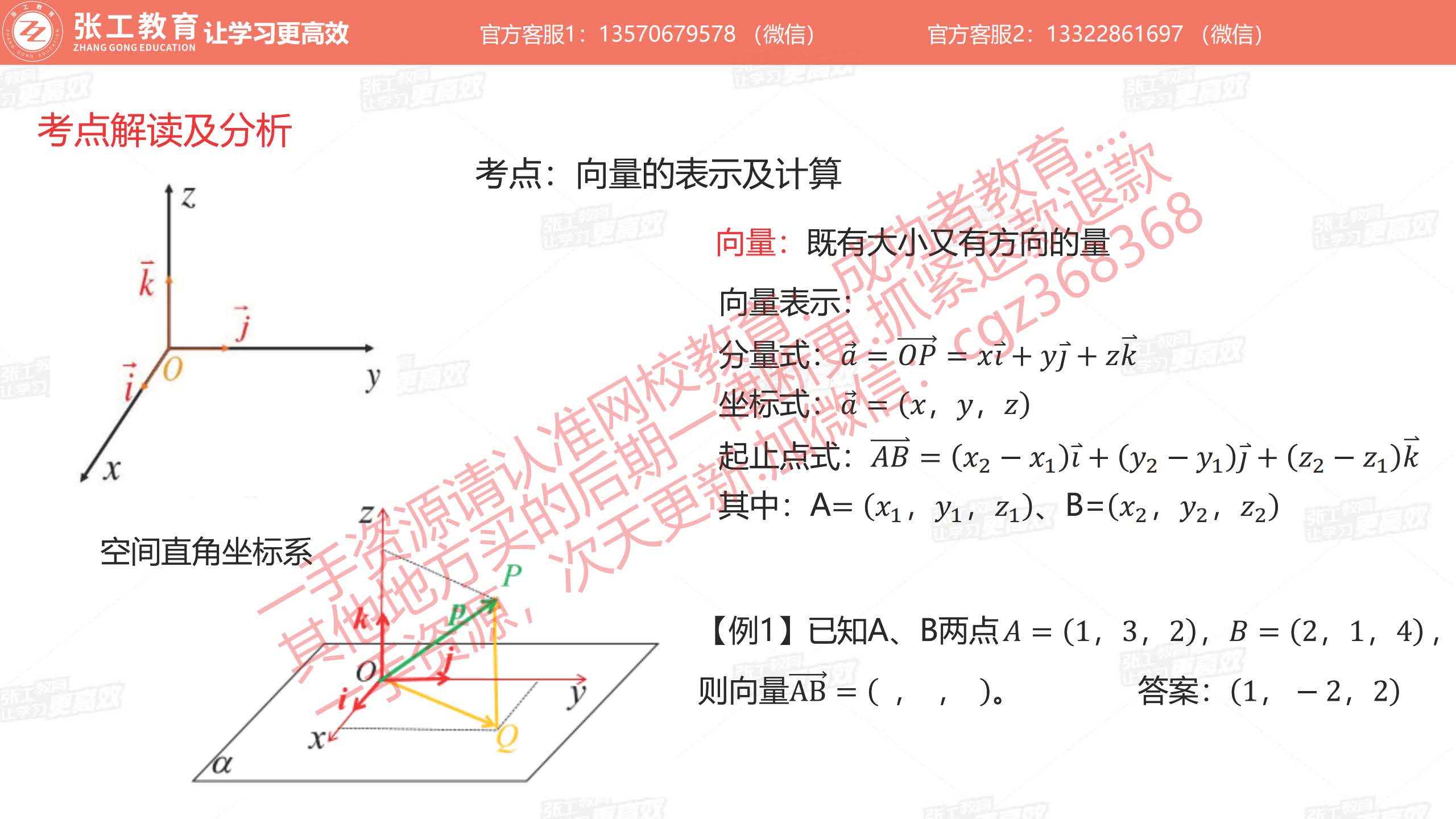
向量及其运算（1分）

• 向量的表示及计算
• 向量的模、单位化、方向角
• 向量的基本运算（加法、减法、数乘）；平行的等价条件
• 向量的数量积（点乘）、运算规律
• 向量的向量积（叉乘）
• 向量的运算规律
• 向量的混合积

空间平面

• 平面的定义、法向量、点法式方程、一般式方程、特殊平面方程
• 平面的截距式方程
• 两平面的夹角、位置关系

空间直线

• 直线的定义、方向向量、点向式方程、参数方程、一般方程
• 两直线的夹角、位置关系

直线与平面的位置关系

• 直线与平面的夹角、特殊位置关系
• 平面位置关系、直线平面位置关系的三维展示

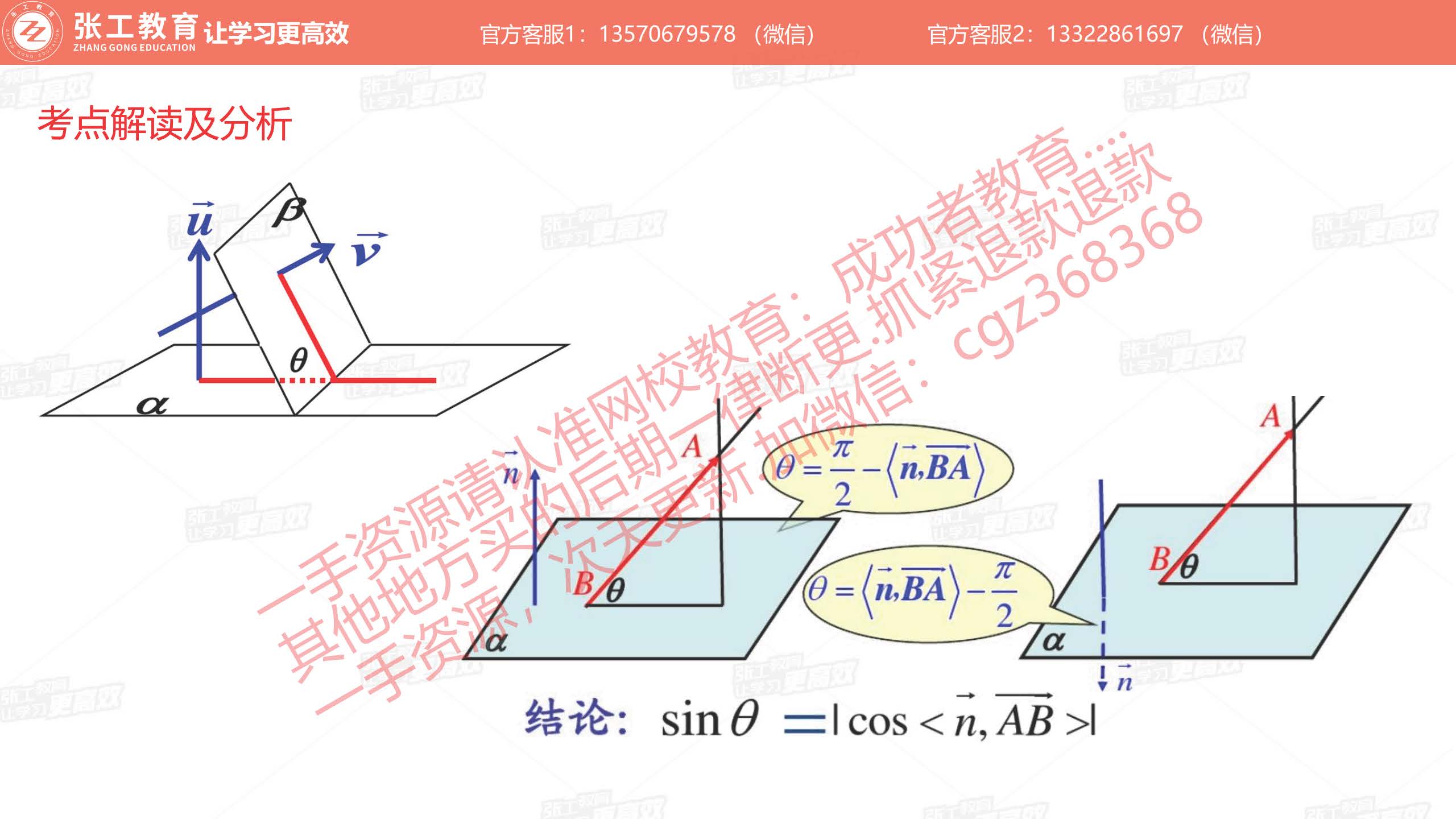
空间曲面、曲线

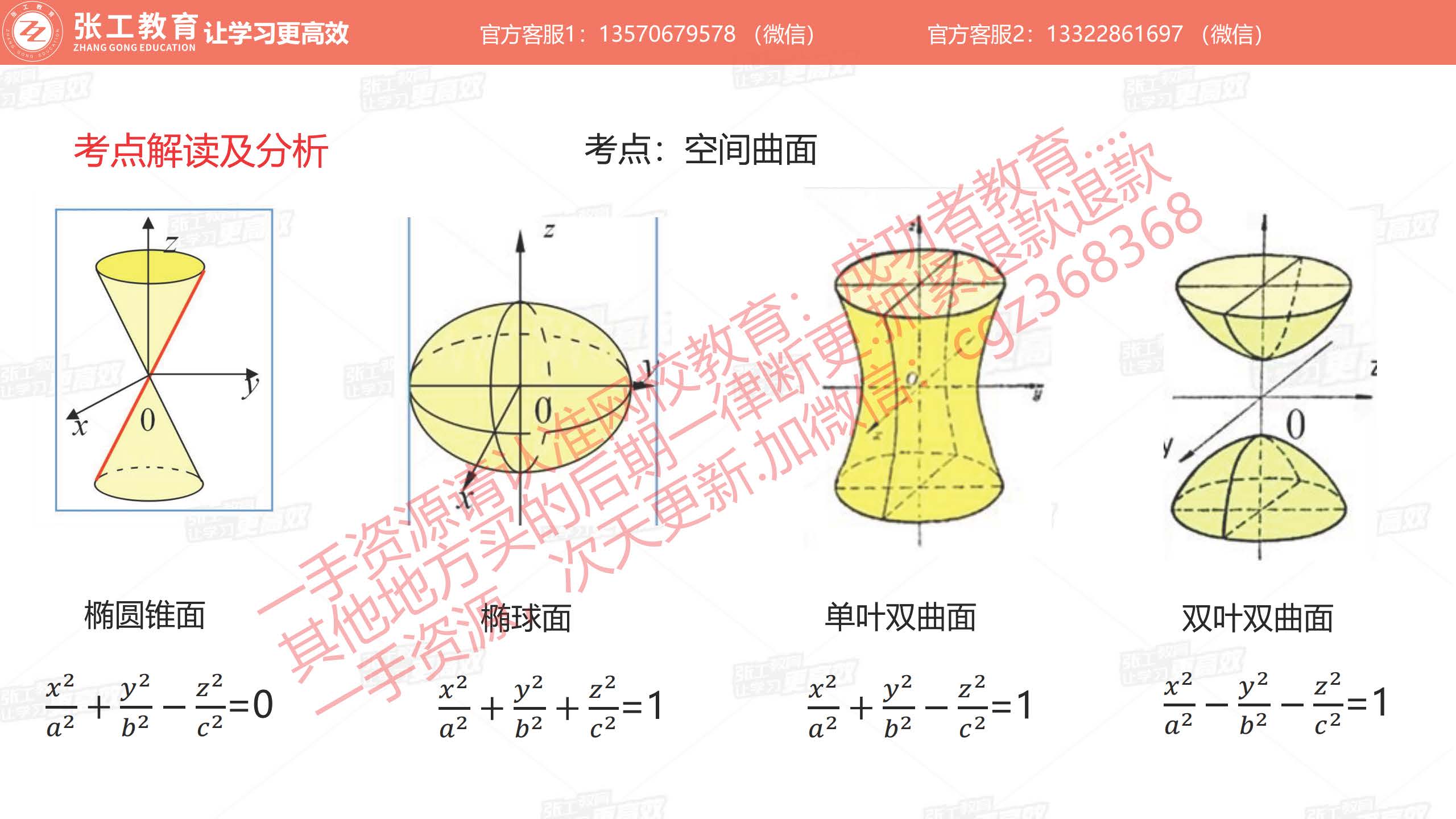
• 常见空间曲面的方程：椭圆锥面、椭球面、单叶双曲面、双叶双曲面
• 柱面：椭圆柱面、双曲柱面、抛物柱面；母线、准线
• 考点分析一：已知曲面方程，识别曲面的形状和名称>>柱面
• 考点分析一：已知曲面方程，识别曲面的形状和名称>>曲面
• 考点分析二：已知曲面是由某平面曲面绕坐标轴旋转所得，求所得旋转曲面方程
• 考点：空间曲线在做表面的投影

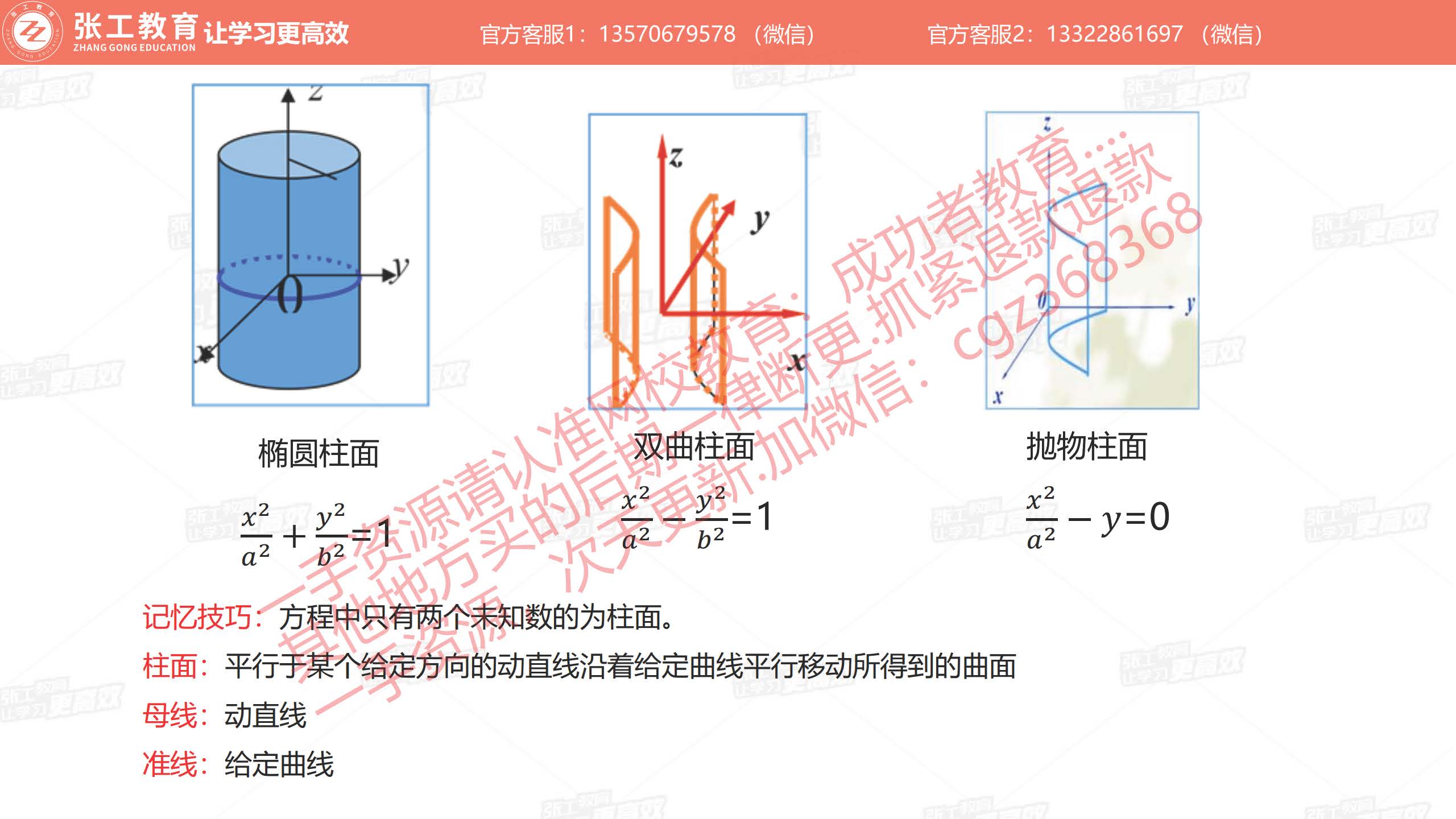
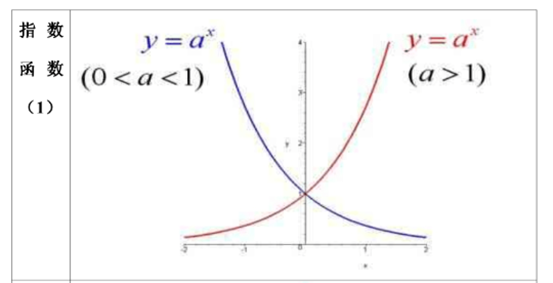
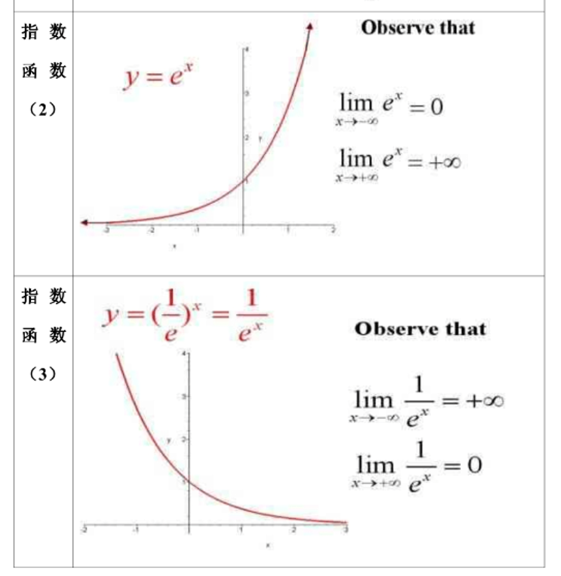
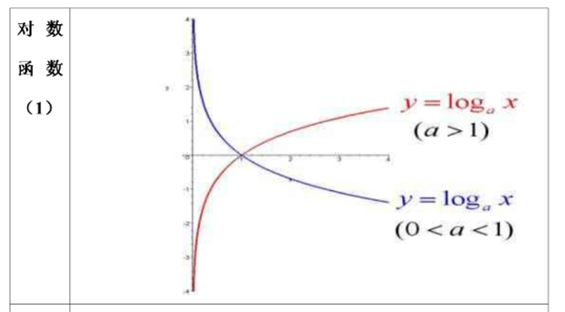
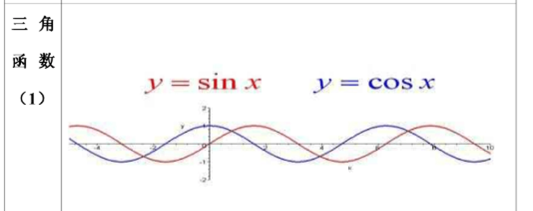
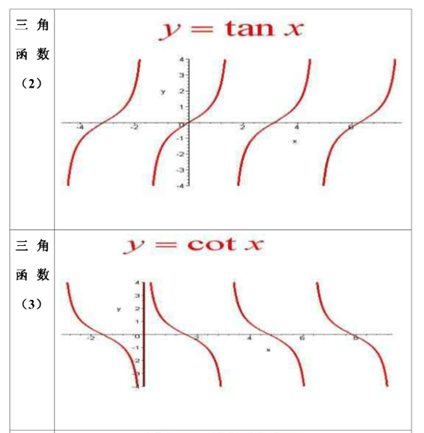
常用函数图像

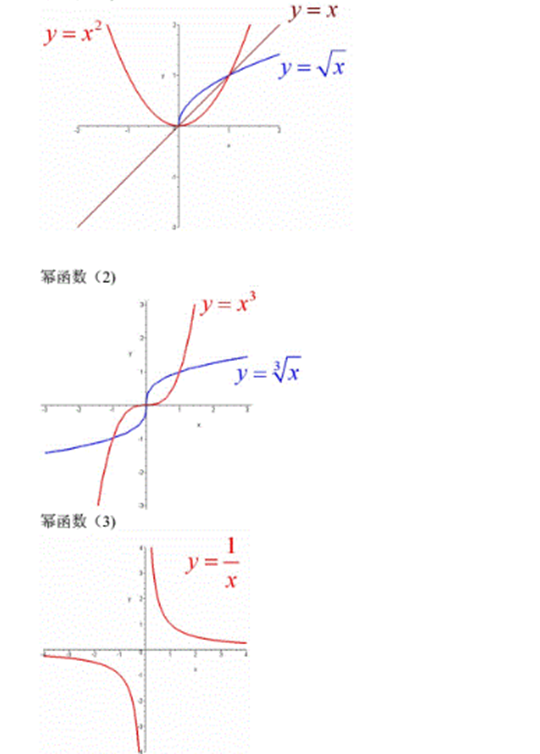
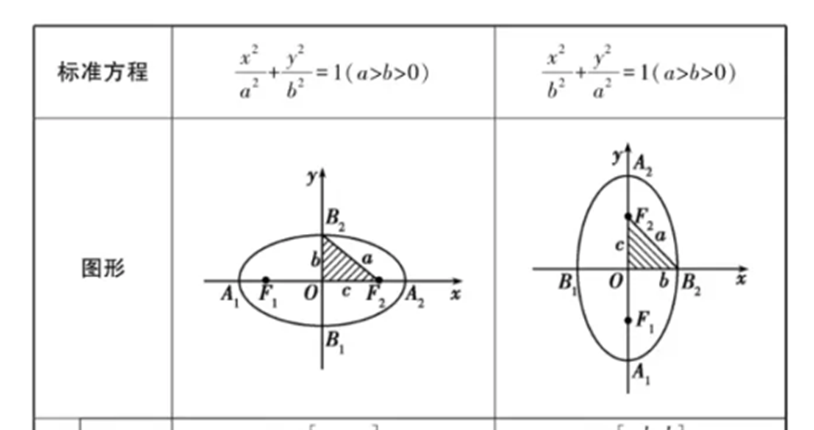
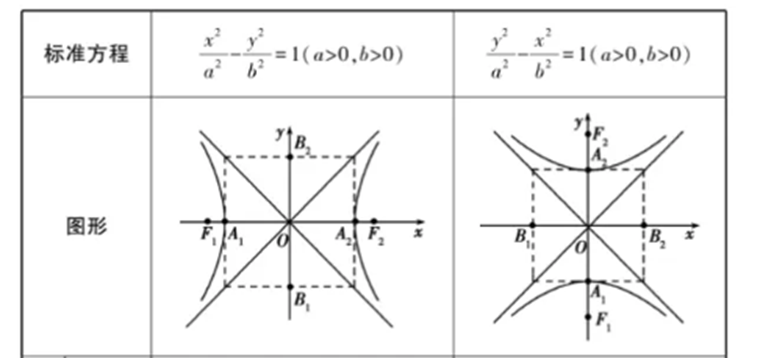
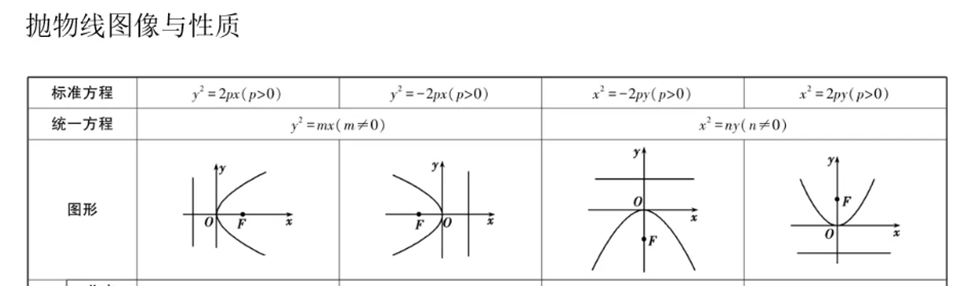
函数极限连续（2分）

难度略大，做好基础知识点，实在太难的题放过。

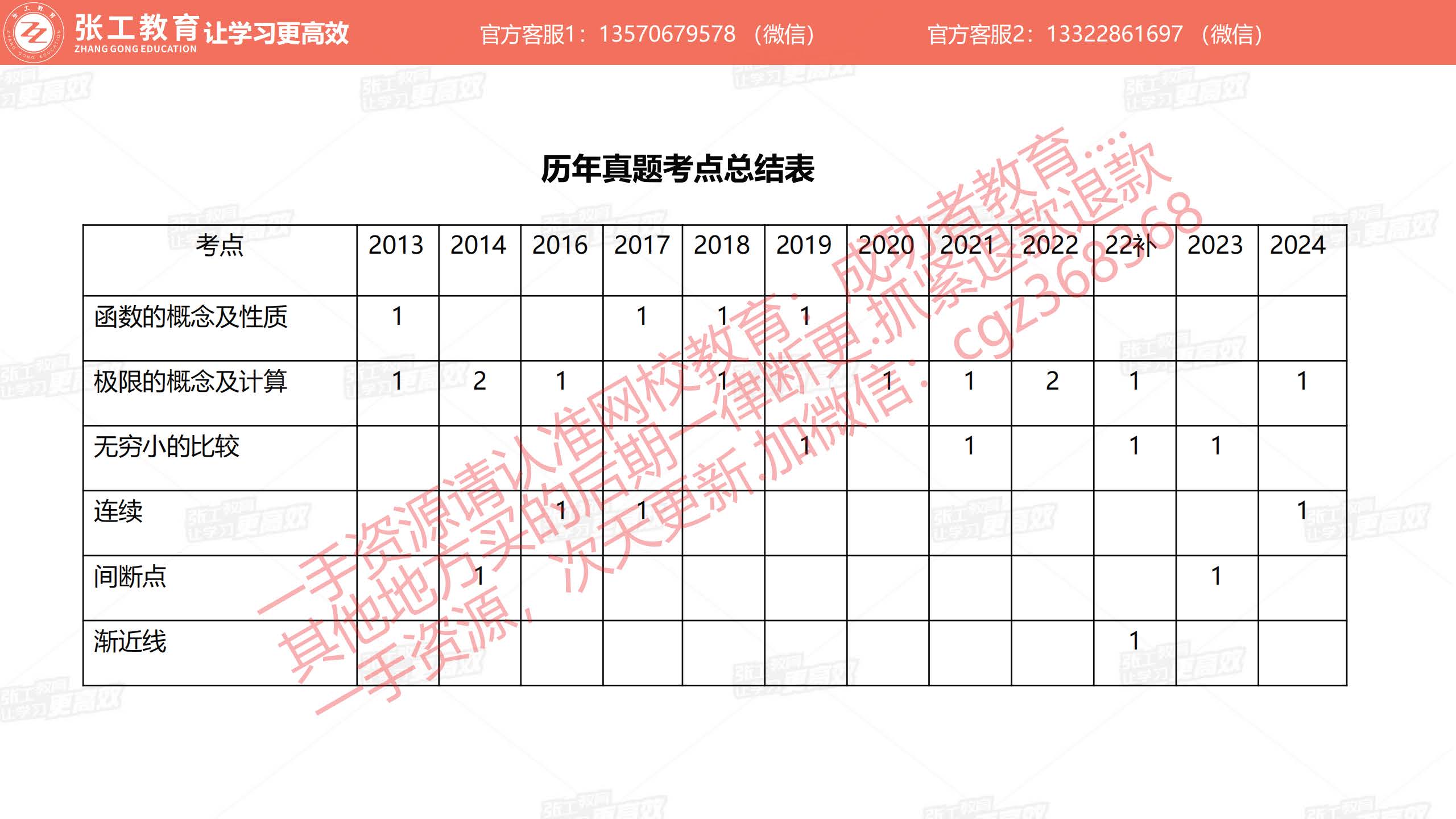
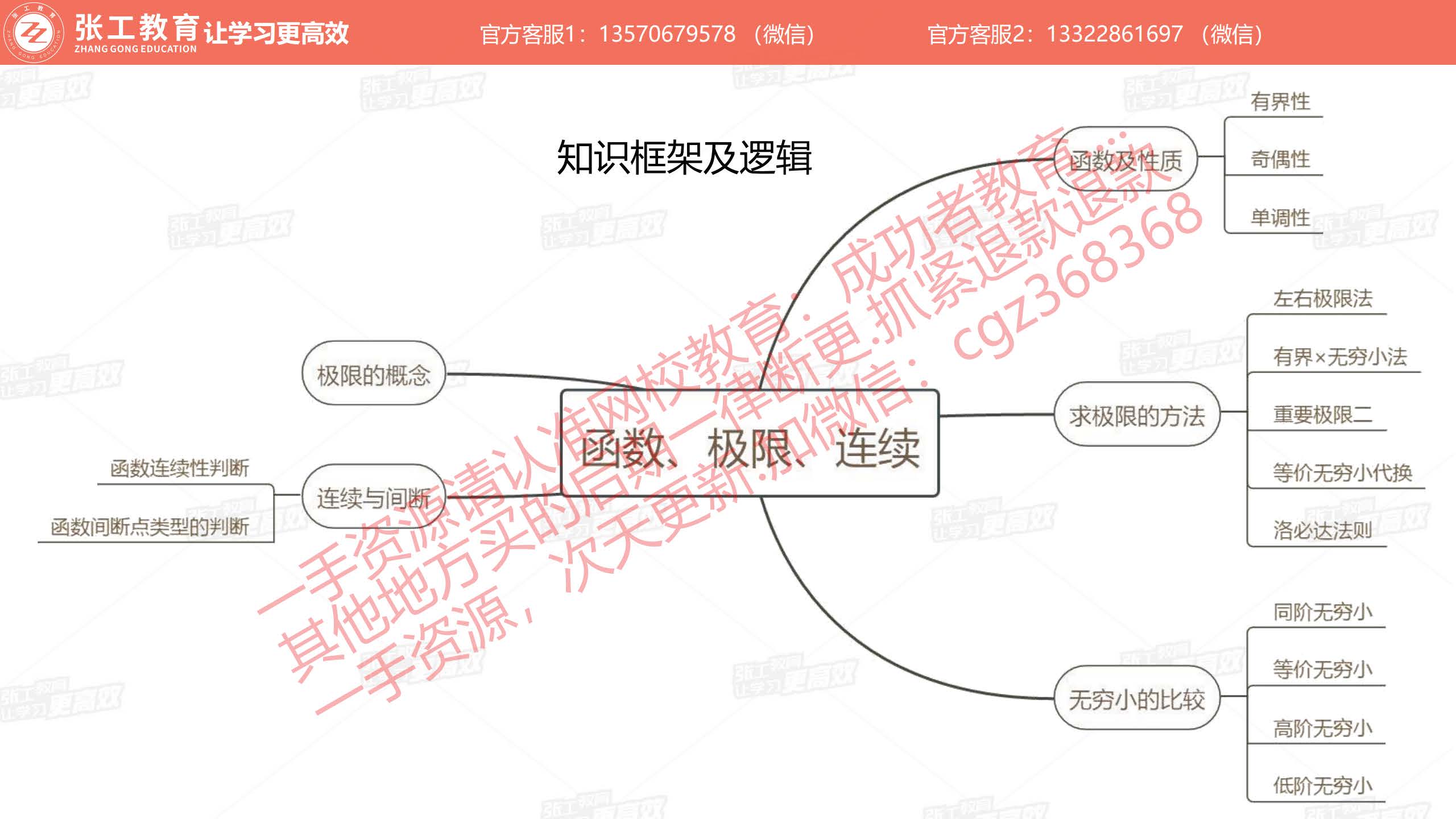
函数的概念及性质

• 函数的概念
  • $y=f(x)$
  • 分段函数
  • 复合函数
  • 反函数
    • $y=f(x)$ 反函数记成 $y=f(x{)}^{-1}$
    • 函数和反函数关于$y=x$对称
• 定义域常见三个限制条件
  • 分母不能为0
  • 偶次根式被开方数大于等于0
  • 真数必须大于0
• 基本初等函数
  • 幂函数
  • 指数函数
  • 对数函数
  • 三角函数
• 常用的运算公式
  • 指数
  • 对数
  • 三角函数
• 函数的性质：奇偶性
  • 条件：定义域关于原点对称
  • 图形特征
• 函数的性质：单调性
• 函数的性质：有界性
  • 上界、下界、有界、充要条件
• 函数的性质：周期性

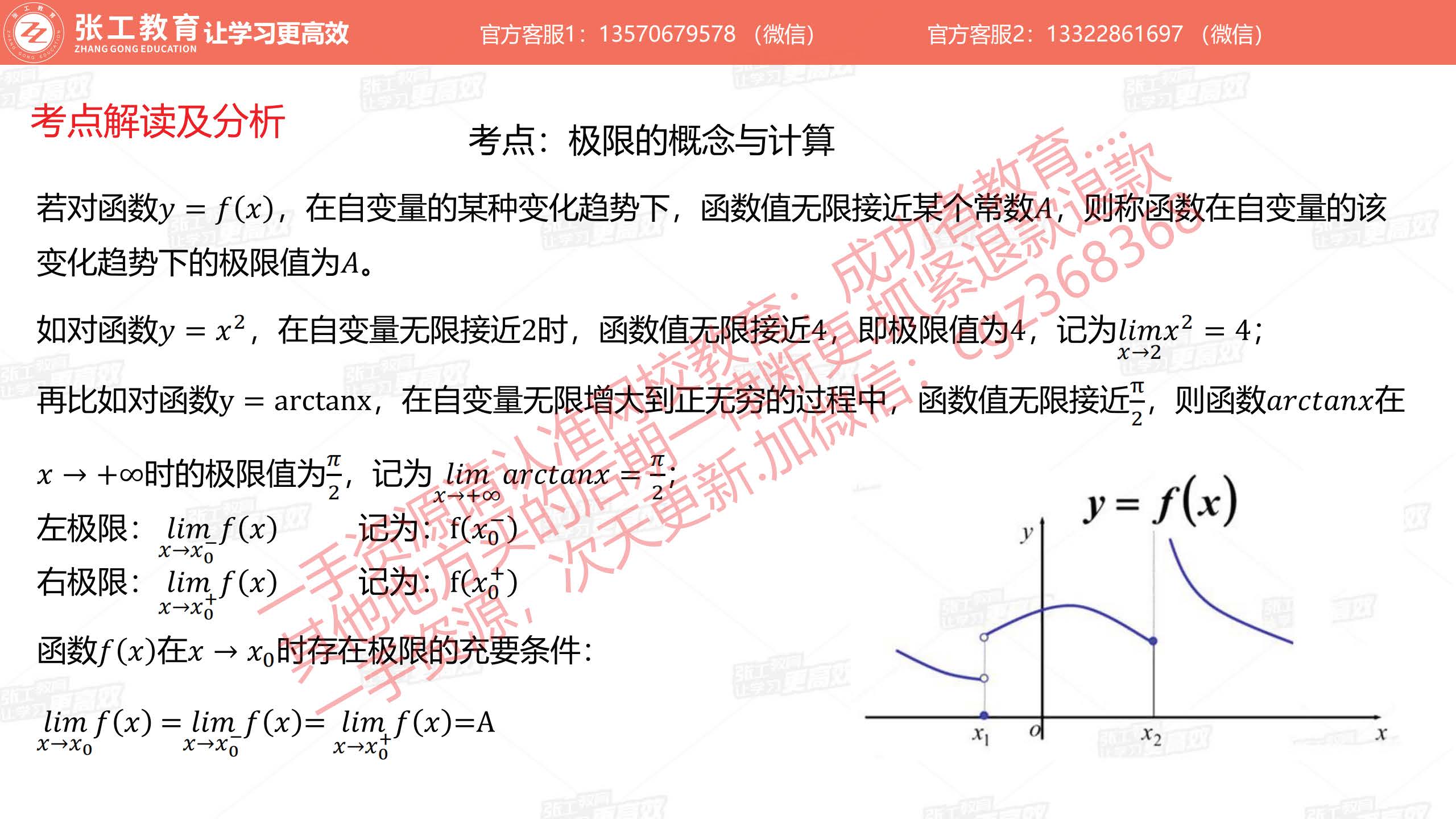
极限的概念及计算（1分）

• 极限的概念
  • 左极限
  • 右极限
  • 极限存在的充要条件
• 极限的计算方法
  • 直接代入法
  • 有界函数乘无穷小
  • 等价无穷小代换（乘除可换、加减不可换）
  • 套用2个重要极限
  • 洛必达法则（一般不用，除非一看就非常简单）

无穷小的比较

• 高阶、低阶、同阶、等价、k阶无穷小

连续

• 连续的定义
• 连续的条件

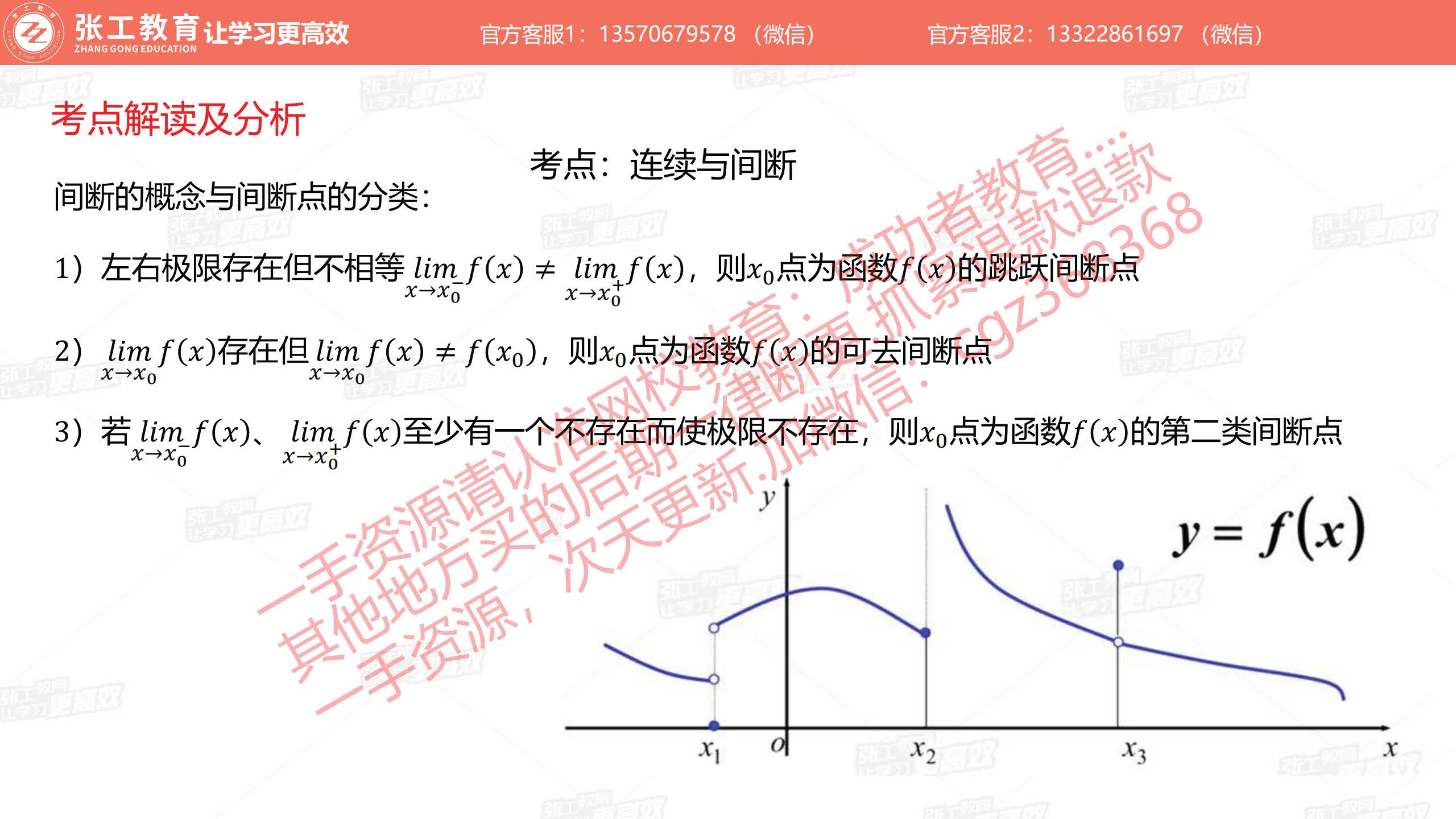
间断点

• 间断的概念
• 间断的分类
  • 跳跃间断点
  • 可去间断点
  • 第二类间断点

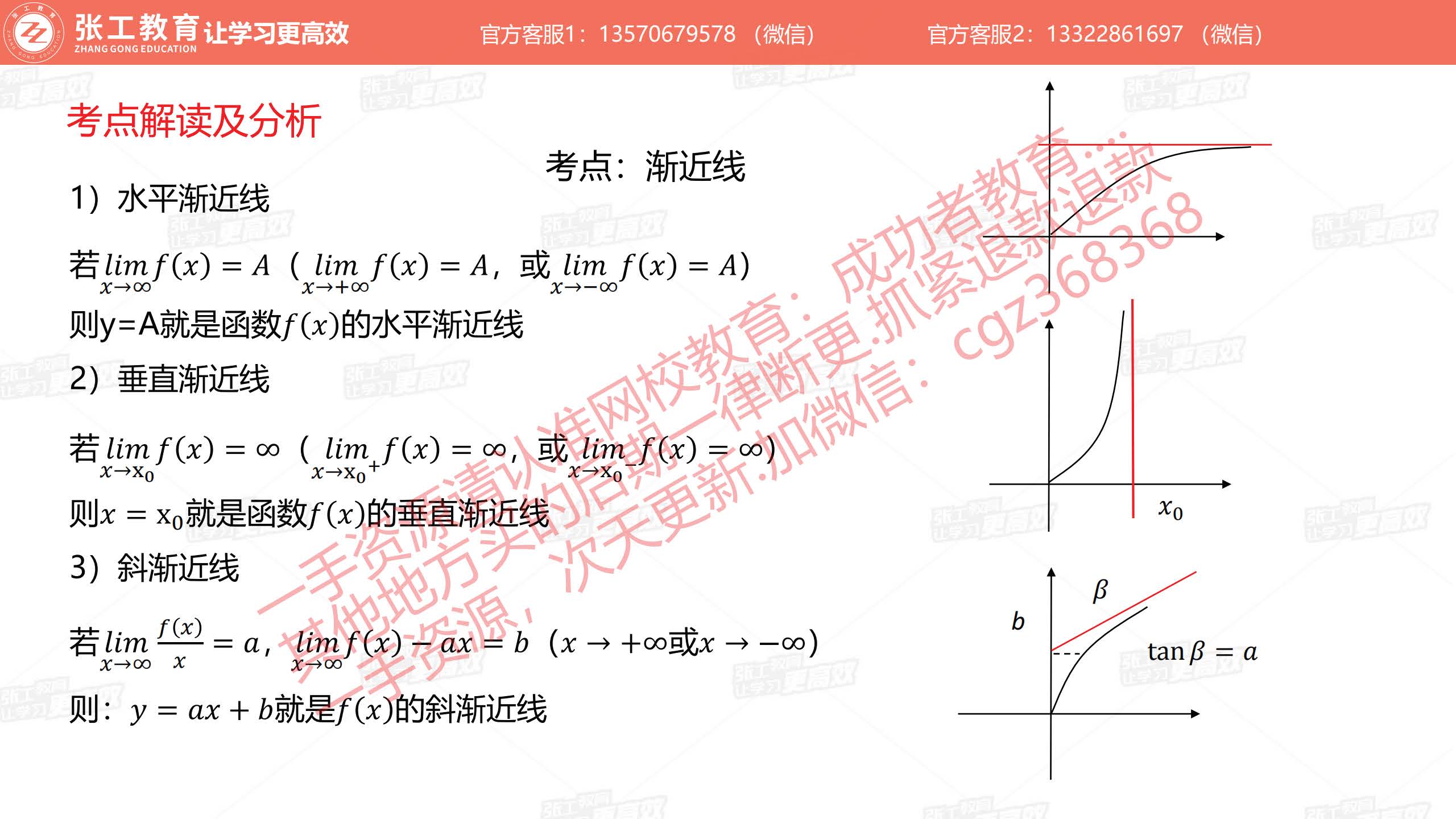
渐近线

• 水平渐近线
• 垂直渐近线
• 斜渐近线

导数与微分（6分）

难度低，易拿分，全拿。

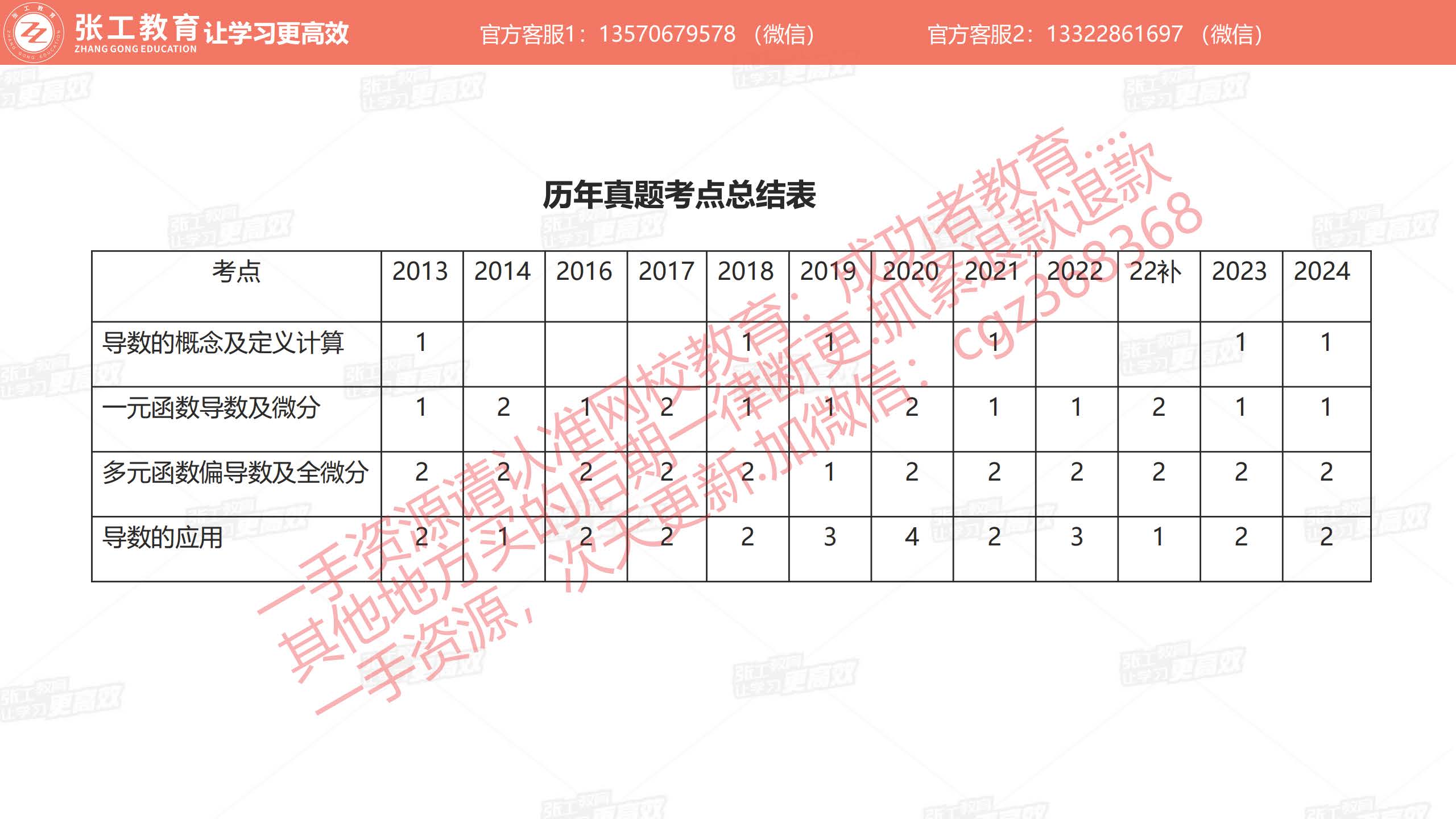
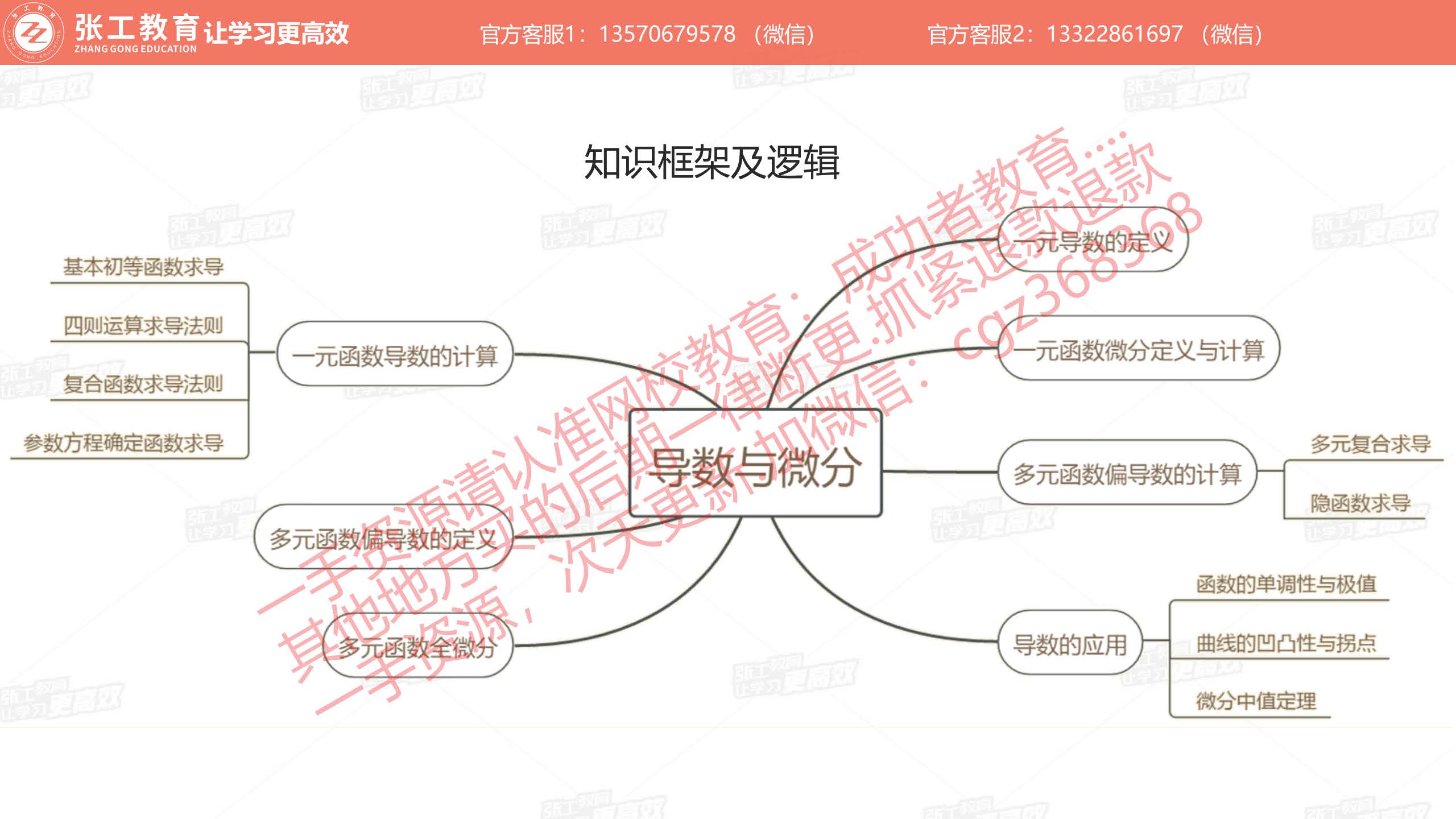
导数的概念及定义计算（0.6分）

• 导数的概念
• 左导数
• 右导数
• 可导的充要条件：左右导数存在且相等
• 必要条件：可导必连续，连续不一定可导

一元函数导数及微分（1.4分）

• 函数求导
  • 基本初等函数导数公式
  • 四则运算求导法则
  • 复合函数求导法则
  • 参数方程函数求导
  • 幂指函数求导
• 微分的概念
• 可微、可导、连续之间的关系

多元函数偏导数及全微分（2分）

• 偏导数的概念
• 偏导数的计算
  • 直接计算
  • 多元复合函数求偏导数——链式法则
  • 多元抽象复合函数求偏导数——链式法则
  • 隐函数求导（偏导）
  • 高阶偏导
• 全微分概念（可微）
  • $dz=f_x^{{}^{\prime }}dx+f_y^{{}^{\prime }}dy$
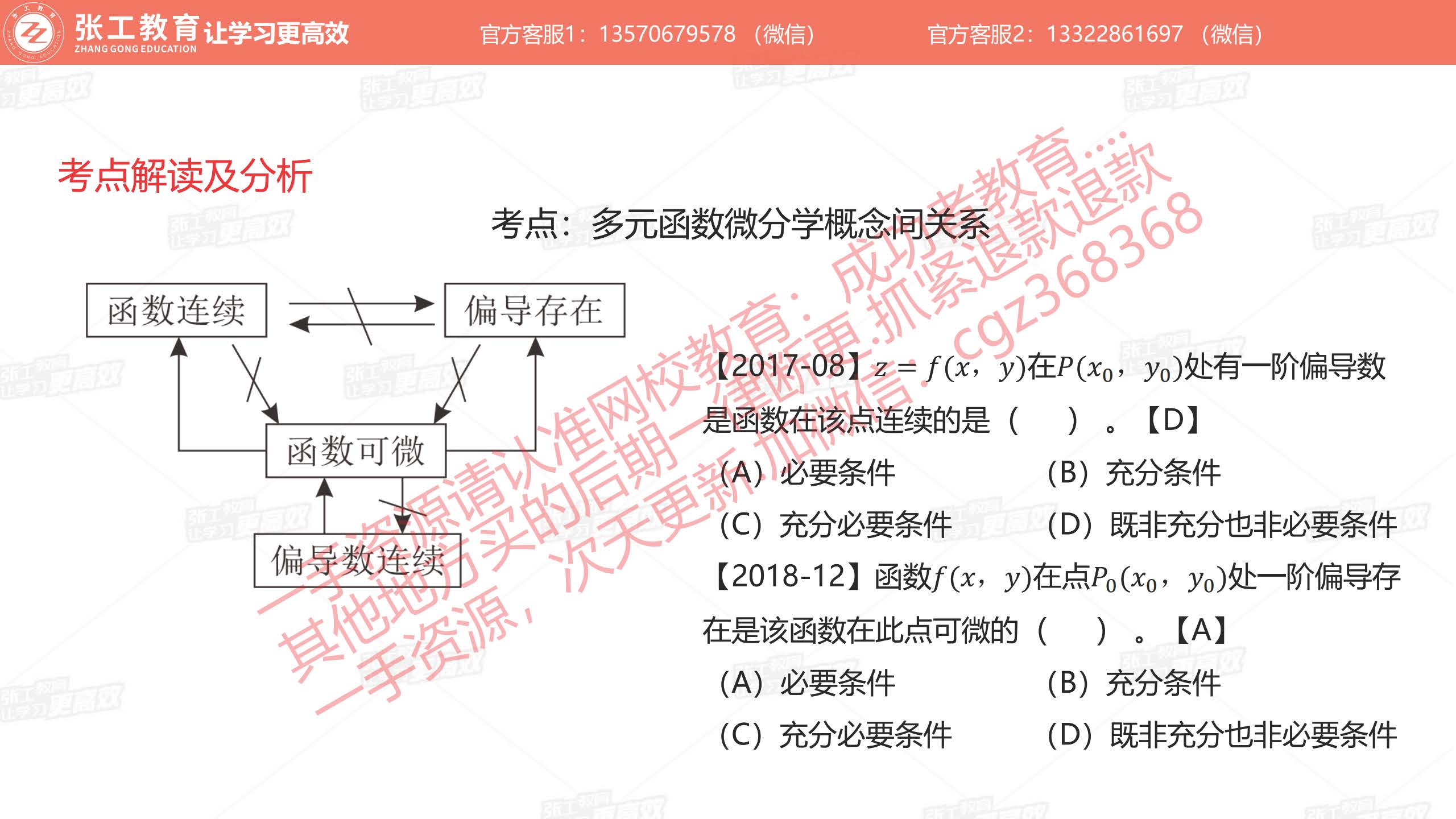
• 多元函数微分学概念之间关系
  • 函数连续、偏导数存在
  • 函数可微
  • 偏导数连续

导数的应用（2分）

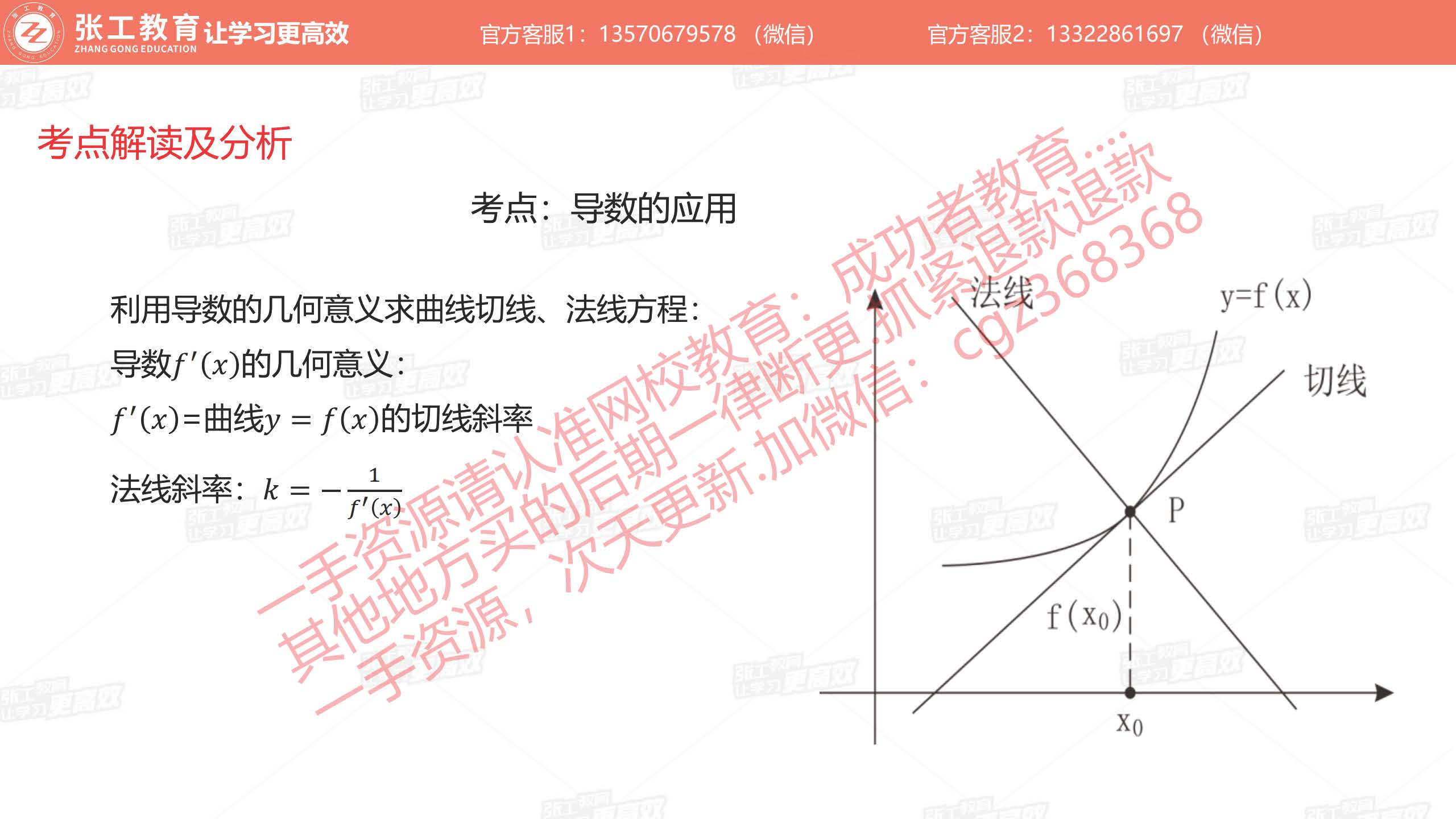
• 求曲线切线、法线方程
  • 切线斜率: $f^{{}^{\prime }}(x)$
  • 法线斜率: $k=-\frac{1}{f^{{}^{\prime }}(x)}$
• 判断一元函数的单调性、驻点
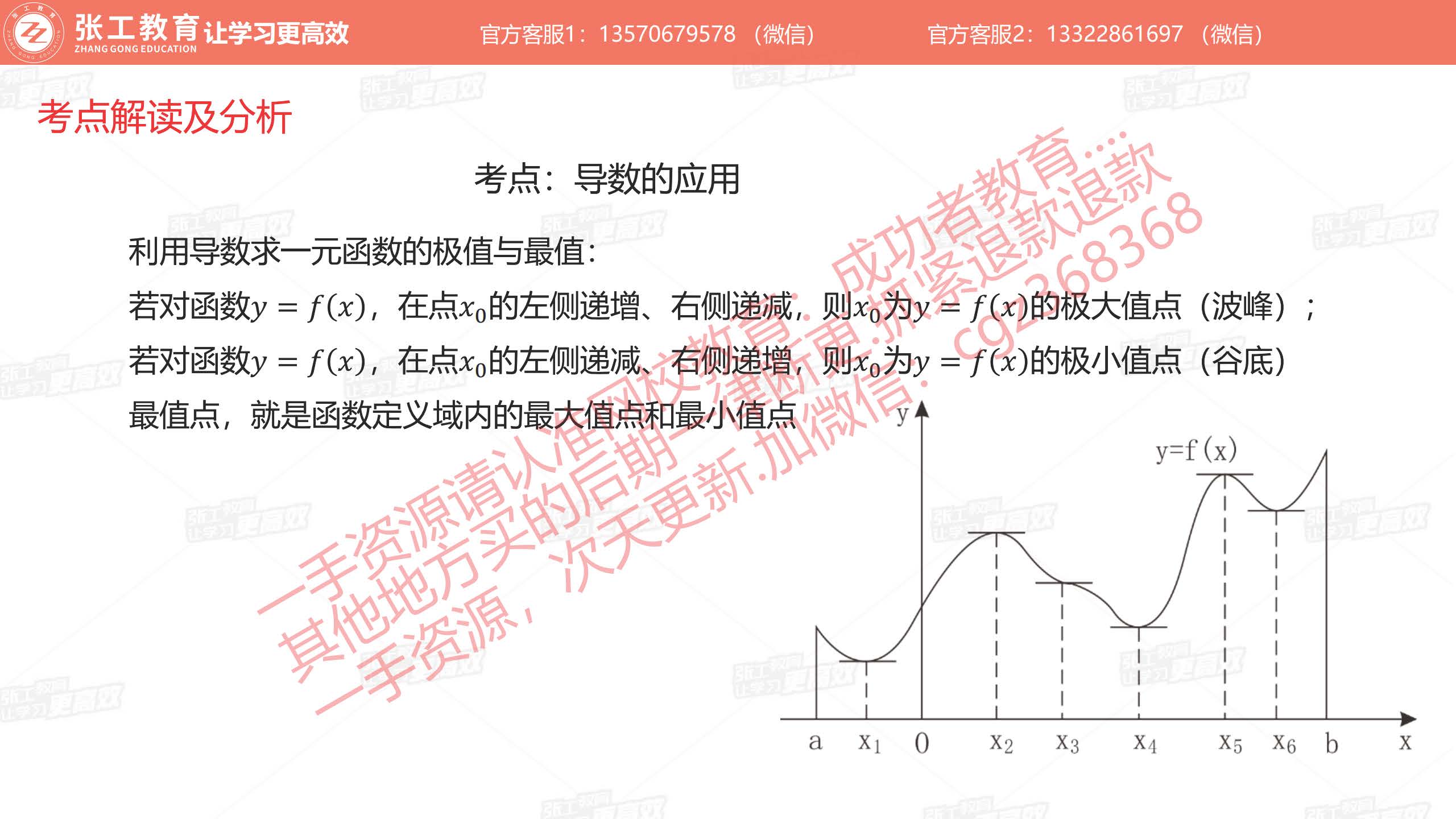
• 求一元函数的极值、最值
• 常用结论（5个）
  • 所有可能得极值点都存在于驻点和不可导点处
  • 可导的极值点必为驻点
  • 导数等于0的点未必是极值点
  • 闭区间上的连续函数的最值仅存在于区间的端点和极值点处
  • 开区间上的最值必为极值
• 求一元函数的凹凸区间、拐点
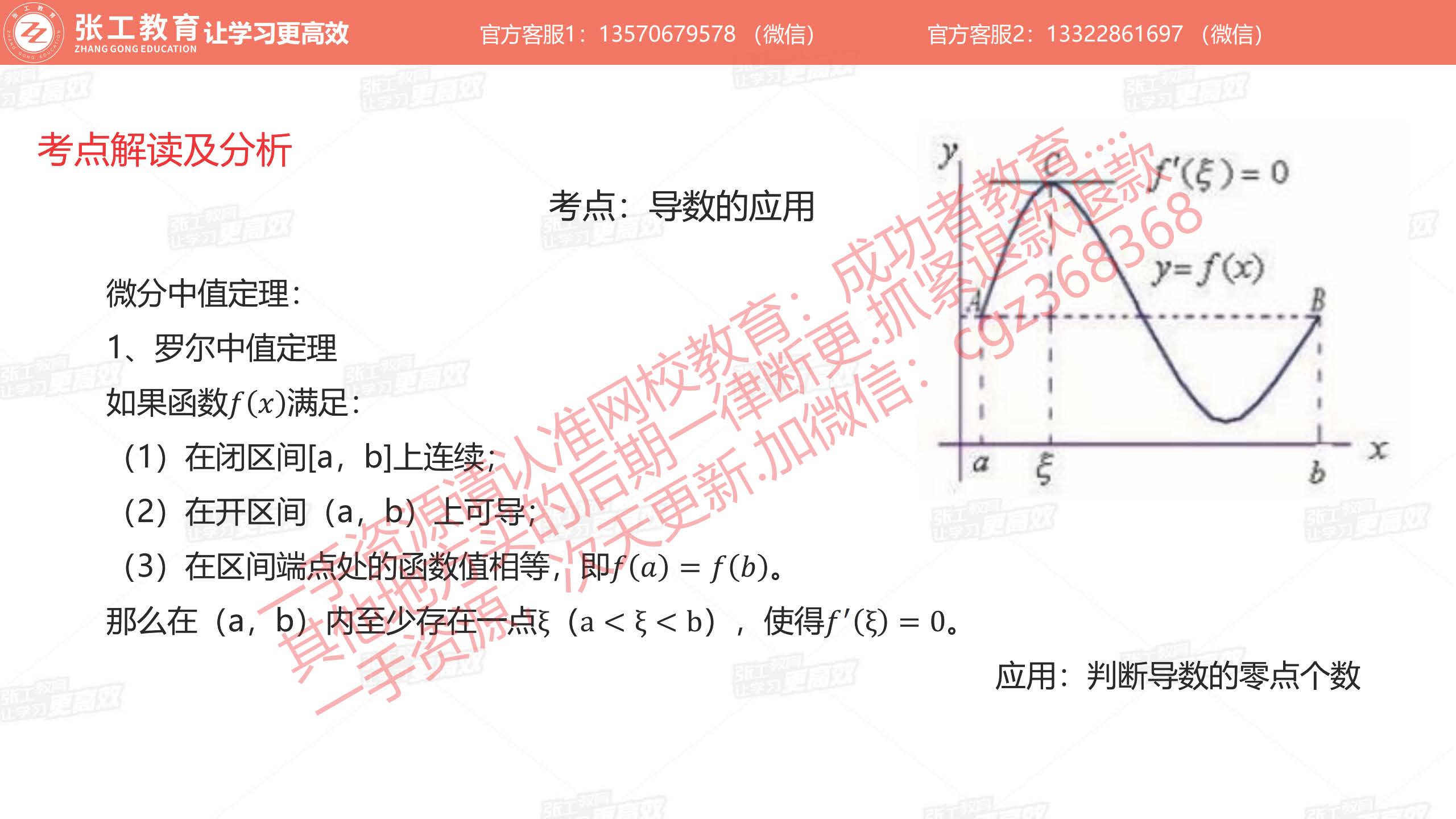
• 微分中值定理（$[a,b]$闭区间连续、$(a,b)$开区间可导）
  • 罗尔中值定理：$f^{{}^{\prime }}(\xi )=0$
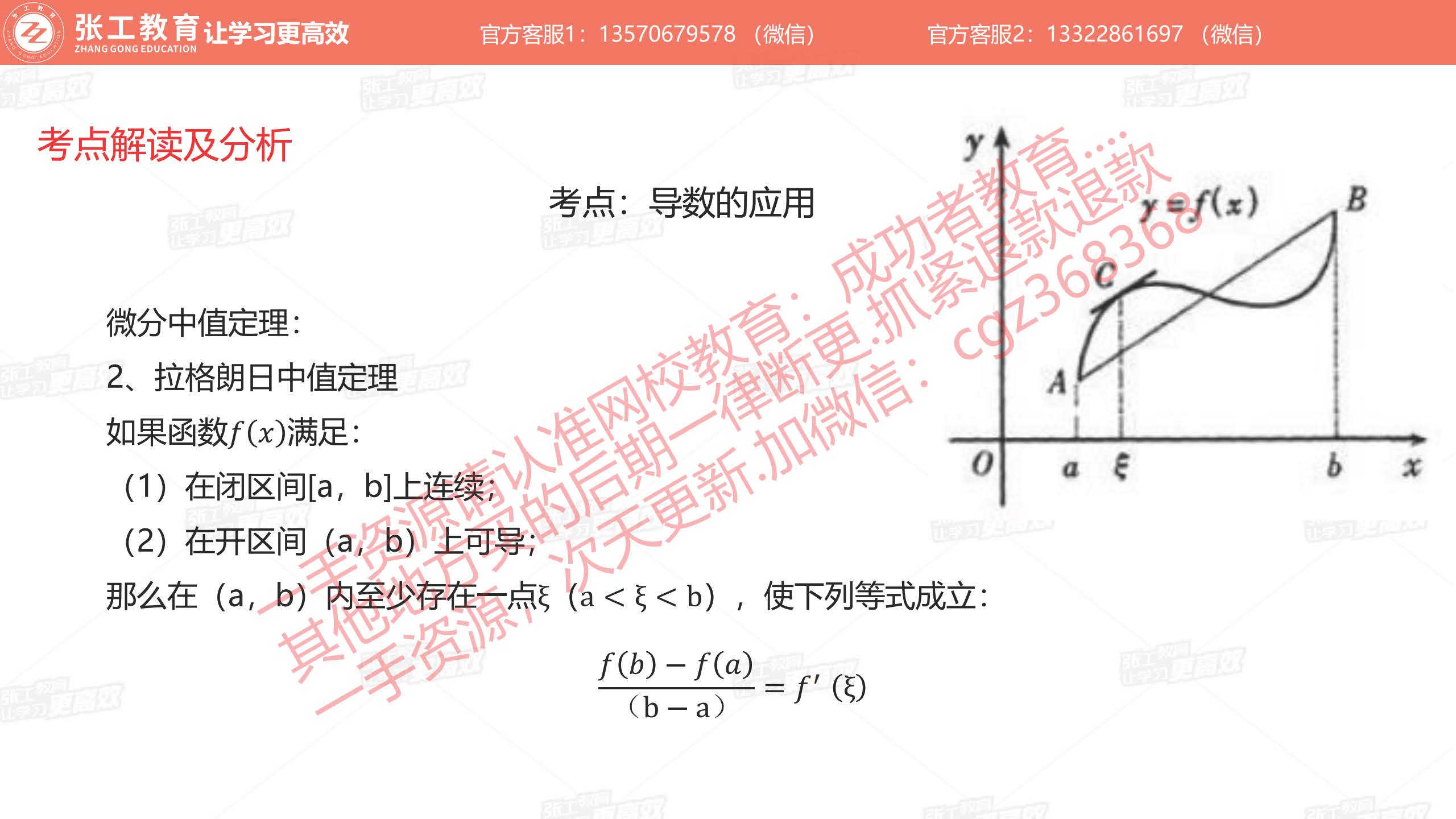
  • 拉格朗日中值定理：$f^{{}^{\prime }}(\xi )=\frac{f(b)-f(a)}{b-a}$
• 偏导数求二元函数的极值
  • $AC-B^2>0$ 必是极值点，A>0极小值，A<0极大值
  • $AC-B^2<0$ 必不是极值点
  • $AC-B^2=0$ 无法判断

积分学（4分）

难度低，易拿分，全拿。

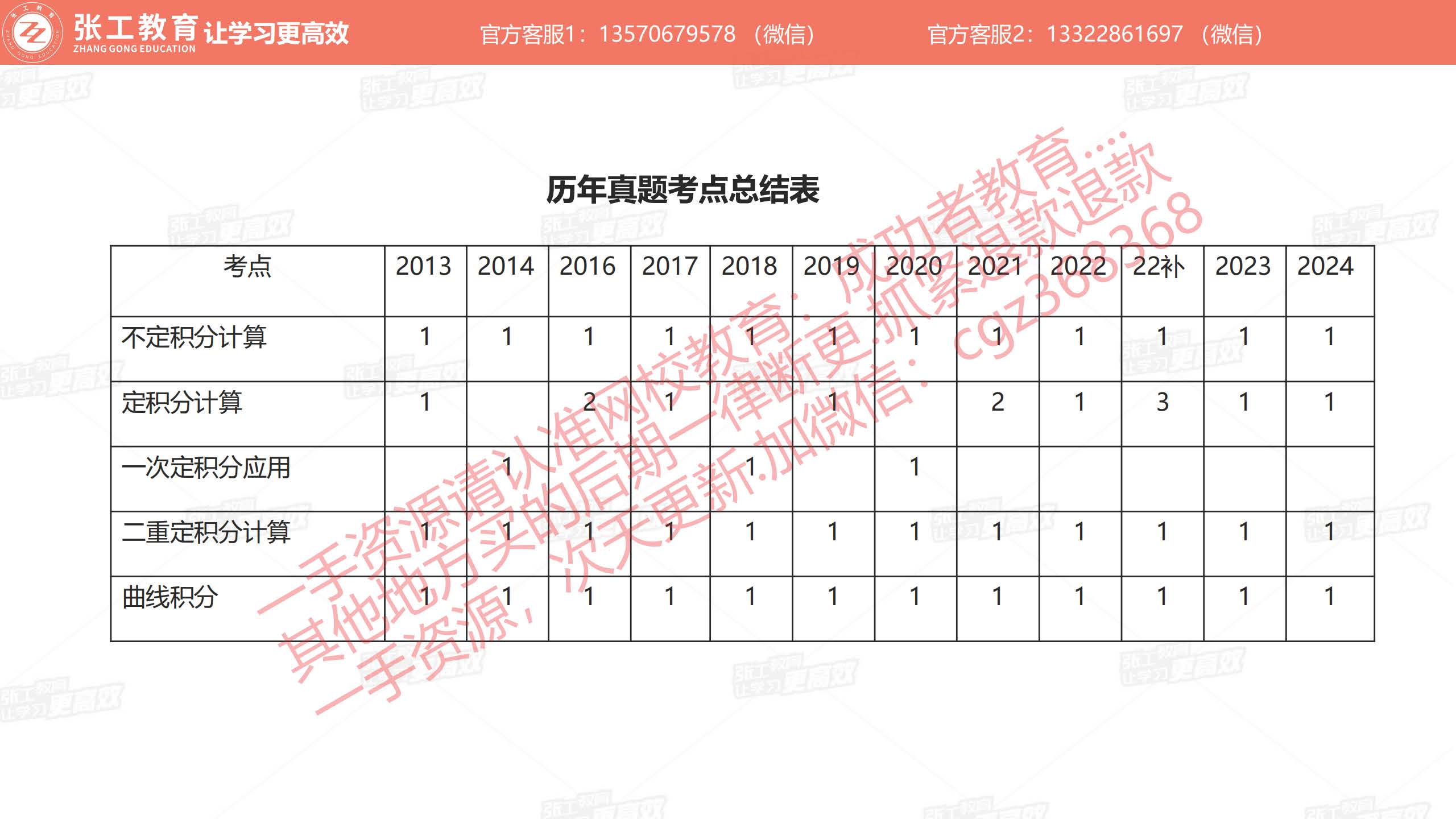
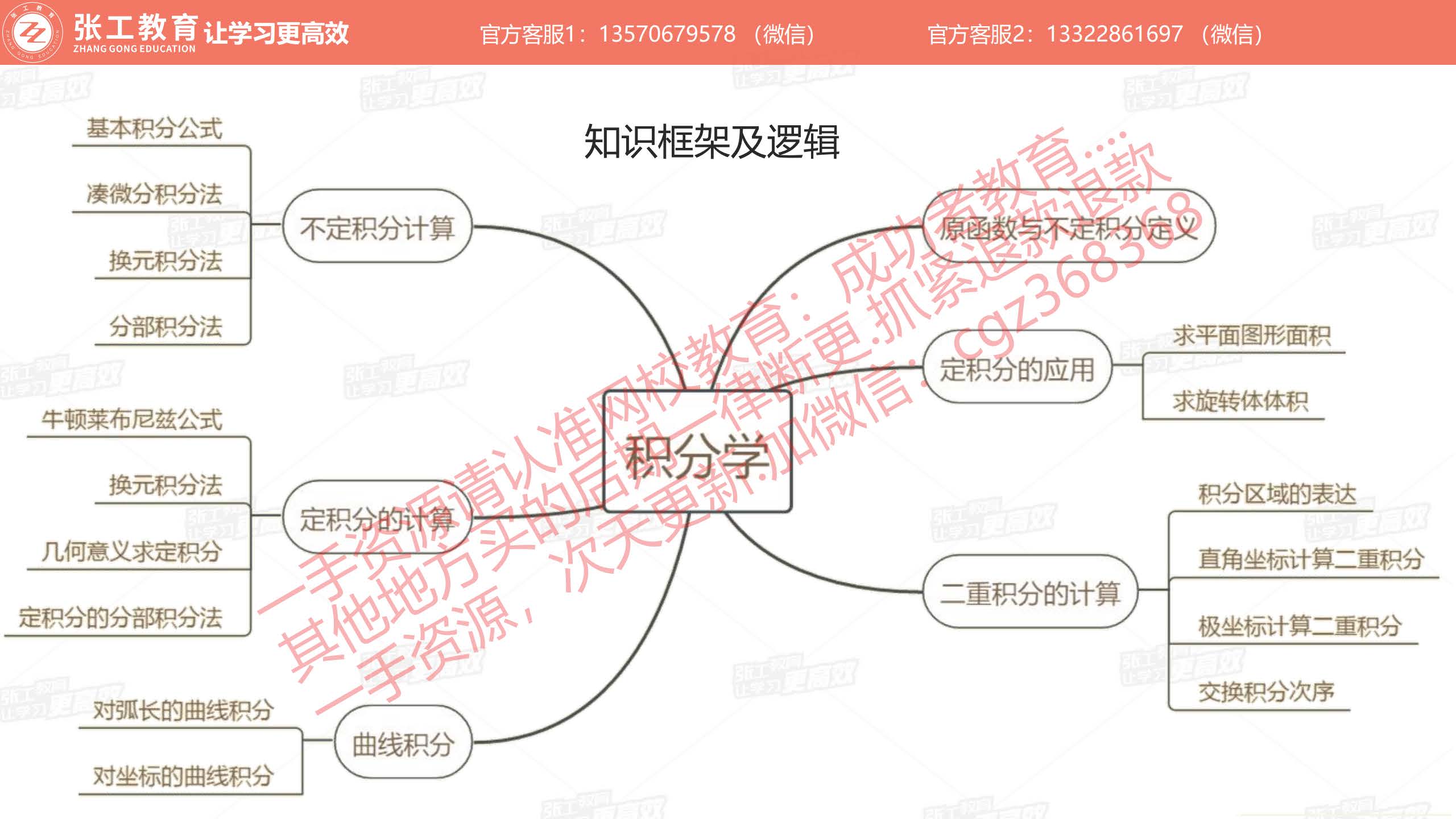
不定积分计算（1分）

• 原函数
• 不定积分的概念
• 不定积分的性质
• 不定积分的计算
  • 基本积分公式
  • 凑微分换元积分法
  • 第二换元积分法
  • 分部积分法

定积分计算（1.3分）

• 牛顿-莱布尼茨公式
• 定积分性质（3个）
• 积分上限函数的概念
• 积分上限函数的性质
  • 上限代入x上限求导-下限代入x下限求导
• 第二种换元积分法（换元必换限）
• 无穷区间的广义积分
• 无界函数的广义积分（瑕点、瑕积分）

一次定积分应用（0.3分）

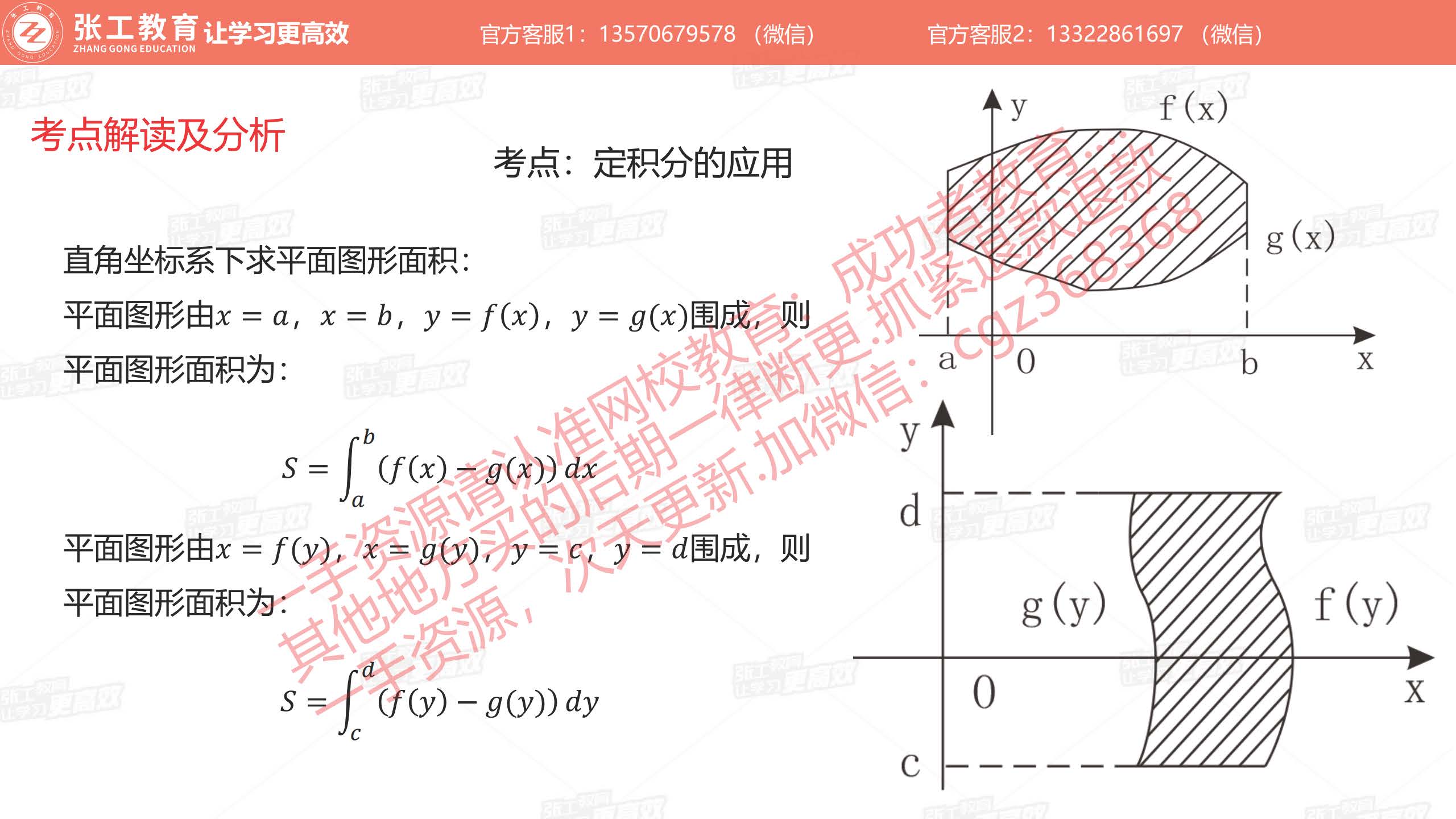
• 直角坐标系下求平面图形的面积
• 极坐标系下求平面图形的面积
• 极坐标与直角坐标的转换
• 极坐标种的常见图形
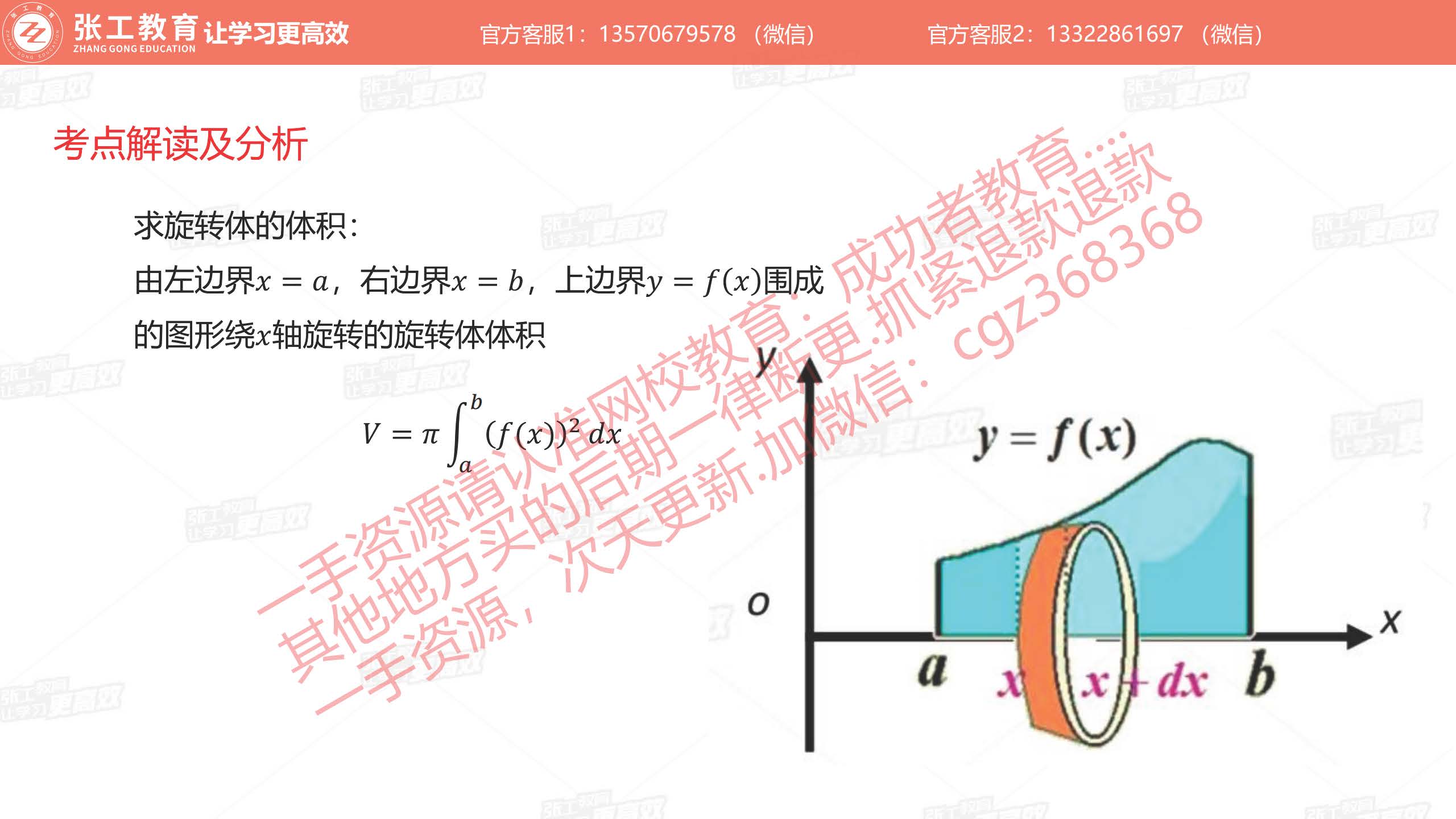
• 求旋转体的体积

二重定积分计算（1分）

• 二重积分的概念和几何意义
• 平面直角坐标系中计算二重积分
• 极坐标系中计算二重积分

曲线积分（1分）

• 对弧长的曲线积分
• 对坐标的曲线积分

微分方程（2分）

难度低，易拿分，全拿。

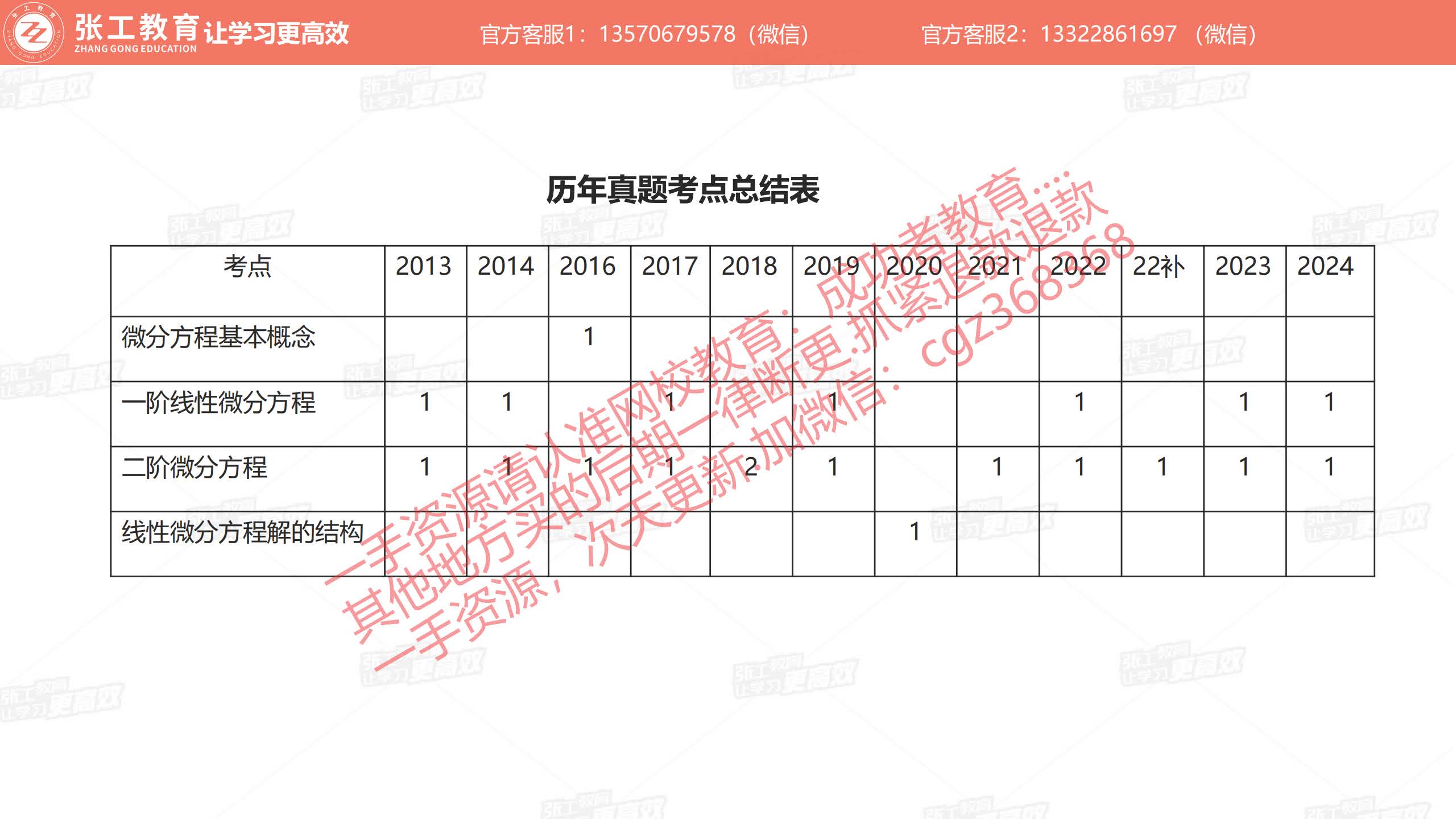
微分方程基本概念（0.1分）

• 概念
• 微分方程的阶
• 微分方程的解
  • 通解
  • 特解

一阶线性微分方程（0.8分）

• 可分离变量的微分方程
• 一阶线性微分方程的通解公式

二阶微分方程（1分）

• $y^{(n)}=f(x)$ 型求解
• 二阶常系数齐次线性微分方程

线性微分方程解的结构（0.1分）

• 一阶线性微分方程
• 二阶线性微分方程
• 二阶常系数非齐次线性微分方程

无穷级数（2分）

略难理解，做好基础知识点，保一挣二。

考试快速做题指南

一般只会让判断是否收敛，不会让算收敛于什么。

做题方法：选项代入、观察法

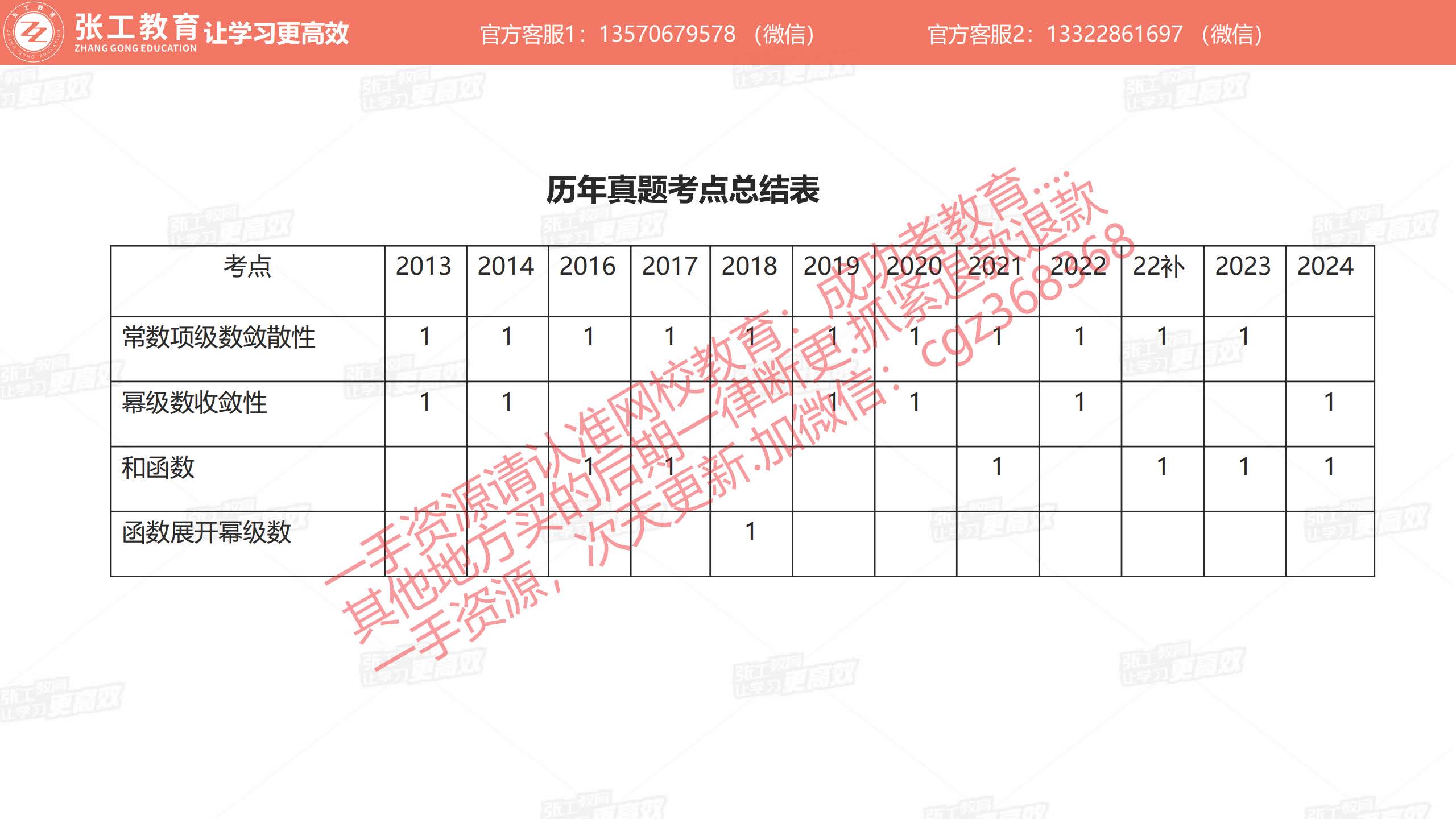
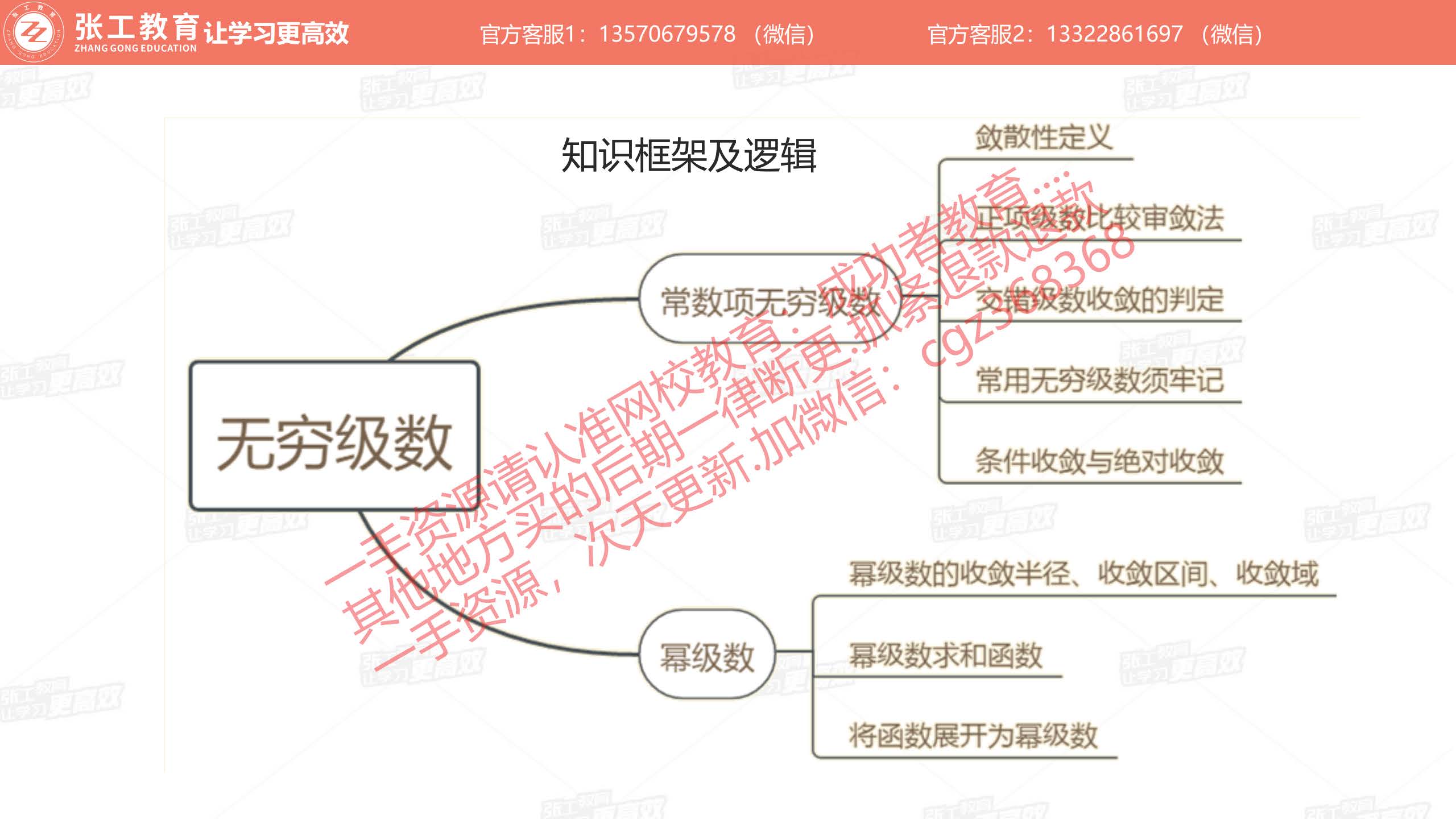
常数项无穷级数（1分）

• 无穷级数的基本概念
• 无穷级数的性质、必要条件、收敛性取决于、充分必要条件
• 交错级数的收敛的充分条件（非必要）
• 常用的两个正项级数：p级数、等比级数
• 正向级数的敛散性判定
  • 比较审敛法
  • “大局观”
  • 数量级
  • 等价无穷小
  • 比值审敛法
• 绝对收敛与条件收敛

考试快速做题指南

有的交错级数也是等比级数，两种判定方法都可以用

幂级数收敛性

考试快速做题指南

幂级数收敛区间、收敛域一般不会缺项，缺项的使用: 选项代入、比值审敛法，例如2019-18

和函数

函数展开幂级数

• 函数展开为幂级数
  • $\frac{1}{1-x}$
  • $e^x$
  • 麦克劳林展开式 $f(x)$
• 傅里叶级数和函数结论

考试快速做题指南

展开成谁的幂级数就先构造谁

傅里叶级数：太难，一般不考，考了就不要这1分了，仅记住傅里叶级数和函数的结论就行了

线性代数（3分）

面太宽，难度低，性价比不高，保二挣三。

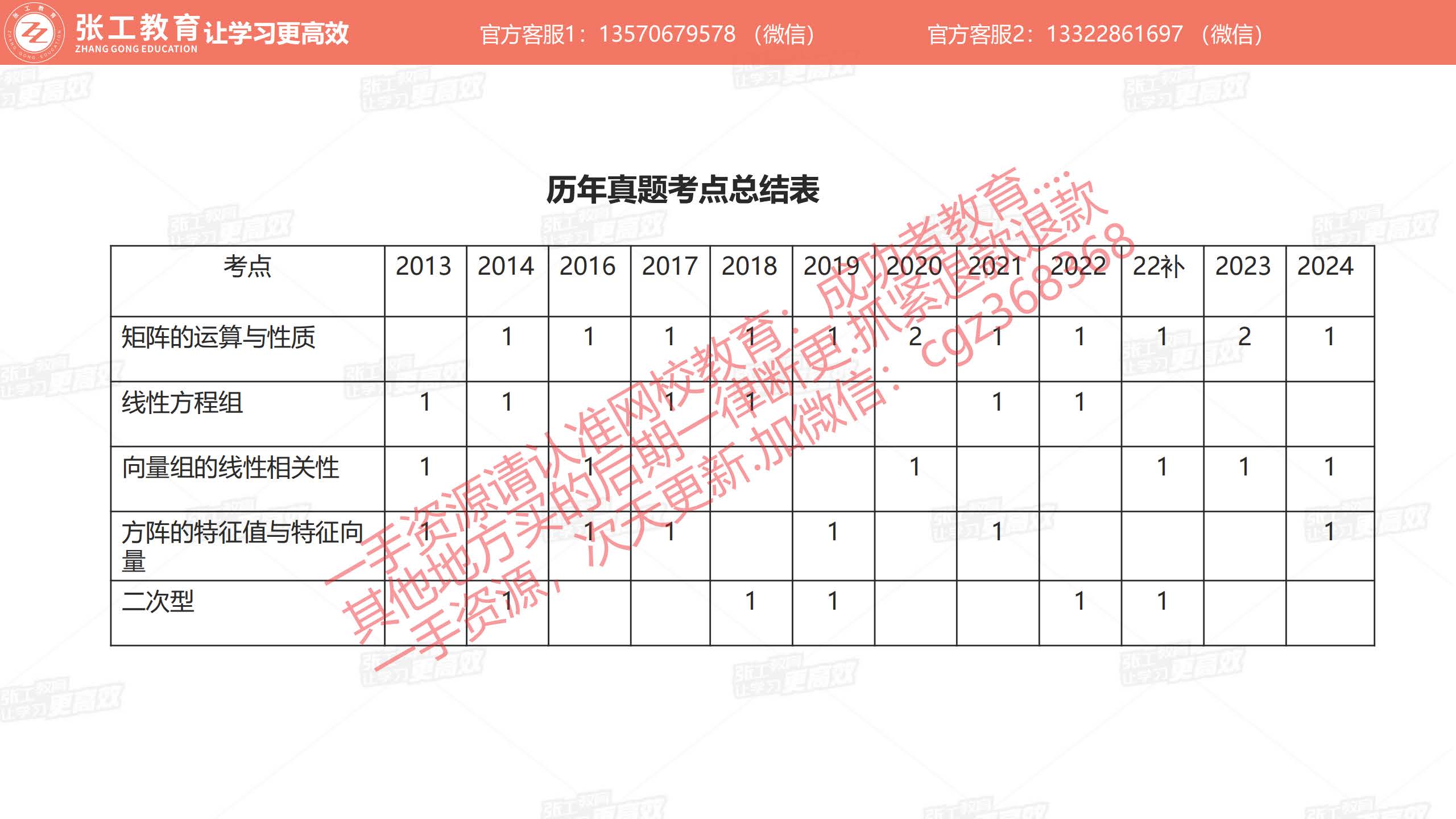
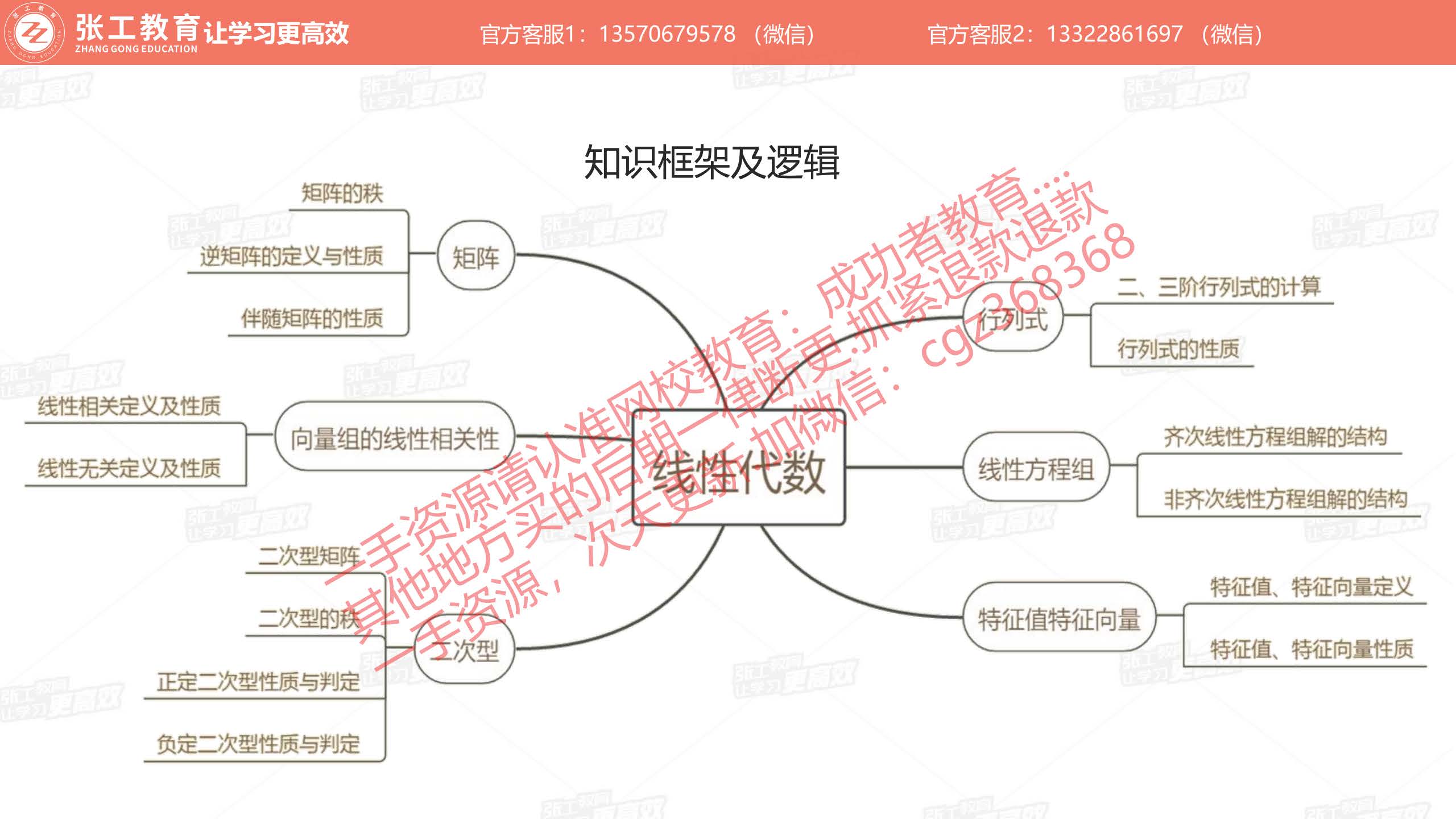
矩阵的运算与性质（1分）

• 二阶、三阶行列式的计算
• 行列式的性质
  • 交换行列式的两行：互为相反数
  • 行列式的某行乘倍数：k倍
  • 行列式的某行的k倍数加到另一行：不变
  • 交换行列式的行列（转置）：不变
  • 以上变换对列一样成立
• 矩阵的概念
• 几种特殊矩阵：
  • 零矩阵、列矩阵、行矩阵、对角阵、阶梯形矩阵
  • 方阵：对角阵、上三角矩阵、下三角矩阵、单位矩阵
• 矩阵的运算种类
  • 加减法、数乘、乘积、转置
  • 初等行交换（唯一不变的是秩）：交换两行、倍乘、倍加
• 矩阵运算的性质
  • 矩阵乘法不满足交换律（单位矩阵除外） $AB\ne BA$
  • 矩阵乘积的转置：$(AB{)}^T=B^T{A}^T$
  • 方阵的行列式性质： $|AB|=|A||B|$
  • $|KA|=K^n|A|$
• 子式的概念（是一种行列式）
• 矩阵的秩的概念
• 矩阵的秩为r的等价条件（4个）
• 矩阵的秩的结论（3个）
• 余子式
• 代数余子式
• 伴随矩阵
• n阶方阵A的伴随矩阵的性质
  • $A{A}^{\ast }=A^{\ast }A=|A|E$
  • $|A^{\ast }|=|A{|}^{n-1}$
  • 伴随矩阵的秩$\{\begin{array}{l}nR(A)=n\\ 1R(A)=n-1\\ 0R(A)<n-1\end{array}$
• 逆矩阵的概念及性质

线性方程组（0.6分）

• 线性方程组的概念与表示
  • 矩阵形式及其简记形式
  • 向量形式及其简记形式
• 系数矩阵、增广矩阵
• 基础概念
  • 线性：未知数都是一次
  • 齐次：右边为0
  • 非齐次：右边不为0
• 齐次线性方程组
  • 只有零解
  • 有非零解
  • 解的结构的主要结论
• 非齐次线性方程组
  • 无解
  • 有唯一解
  • 有无穷多解
• 齐次线性方程组与非齐次线性方程组的关系（3个）

向量组的线性相关性（0.6分）

• 向量组的秩
• 向量组的线性相关的等价条件（5个）
• 向量组的线性无关的等价条件（5个）
• 向量组的极大线性无关组

方阵的特征值与特征向量（0.6分）

• 特征值与特征向量的概念
• 特征值求法
• 特征值与特征向量的性质（5个）
  • 特征值乘积=方阵的行列式
  • 特征值的和=方阵主对角线之和（方阵的迹）
  • 方阵指数、倍、逆矩阵运算同实数的运算
  • 方阵+KE的特征值同实施的运算
  • 不同特征值对应的特征向量正交
• 向量内积
• 相似矩阵的概念
• 相似矩阵的性质（2个）
  • 相似矩阵具有相同的秩和行列式
  • 相似矩阵具有相同的特征值
• 矩阵的相似对角化概念
• 矩阵的相似对角化的条件（2个）
  • n阶方阵具有n个不同的特征值
  • 对于m重根特征值，有m个线性无关的特征向量

二次型（0.6分）

• 二次型的概念
• 二次型的矩阵与二次齐次多项式的互相转换
  • 二次型的矩阵一定是实对称矩阵（至少考试是）
  • 二次型的矩阵主对角线元素对应二次多项式的系数
  • 二次型的矩阵其余元素对应二次多项式的系数
• 二次型矩阵的秩即为二次型的秩
• 二次型标准型的概念
• 二次型标准型求法：配方法、特征值法
• 二次型标准型的结论（3个）、正惯性指数、负惯性指数
• 合同矩阵的概念
• 合同矩阵的结论（2个）
  • n阶方阵A、B有相同的特征值，则A、B合同
  • A、B合同，则正特征值个数相同、负特征值个数相同
• 正定二次型的概念及其等价条件（5个）
  • 等价于A的各阶顺序主子式全为正
• 负定二次型的概念及其等价条件（5个）
  • 等价于A的奇数阶顺序主子式全为负，偶数阶顺序主子式全为正

考试快速做题指南

• 因标准型不唯一，求标准型只看正负惯性指数就行了，如果选项中有一些选项正负惯性指数相同，可快速排除这些选项。
• 正常考试的合同矩阵一定是实对称的，不对称的可以排除。
• 判断正定二次型：一般用各阶顺序主子式全为正。

概率论与数理统计（3分）

面太宽，难度低，性价比不高，保二挣三。

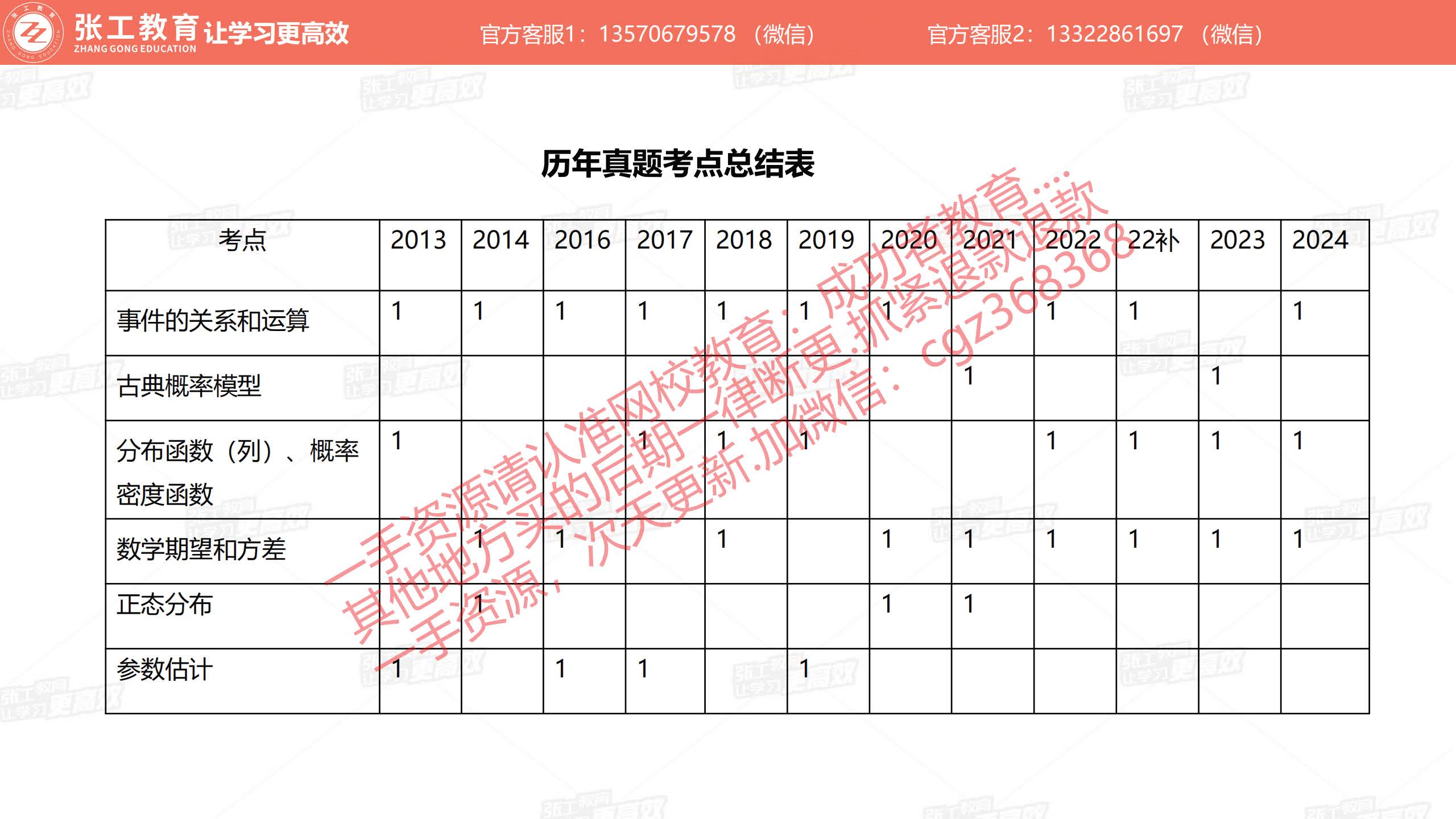
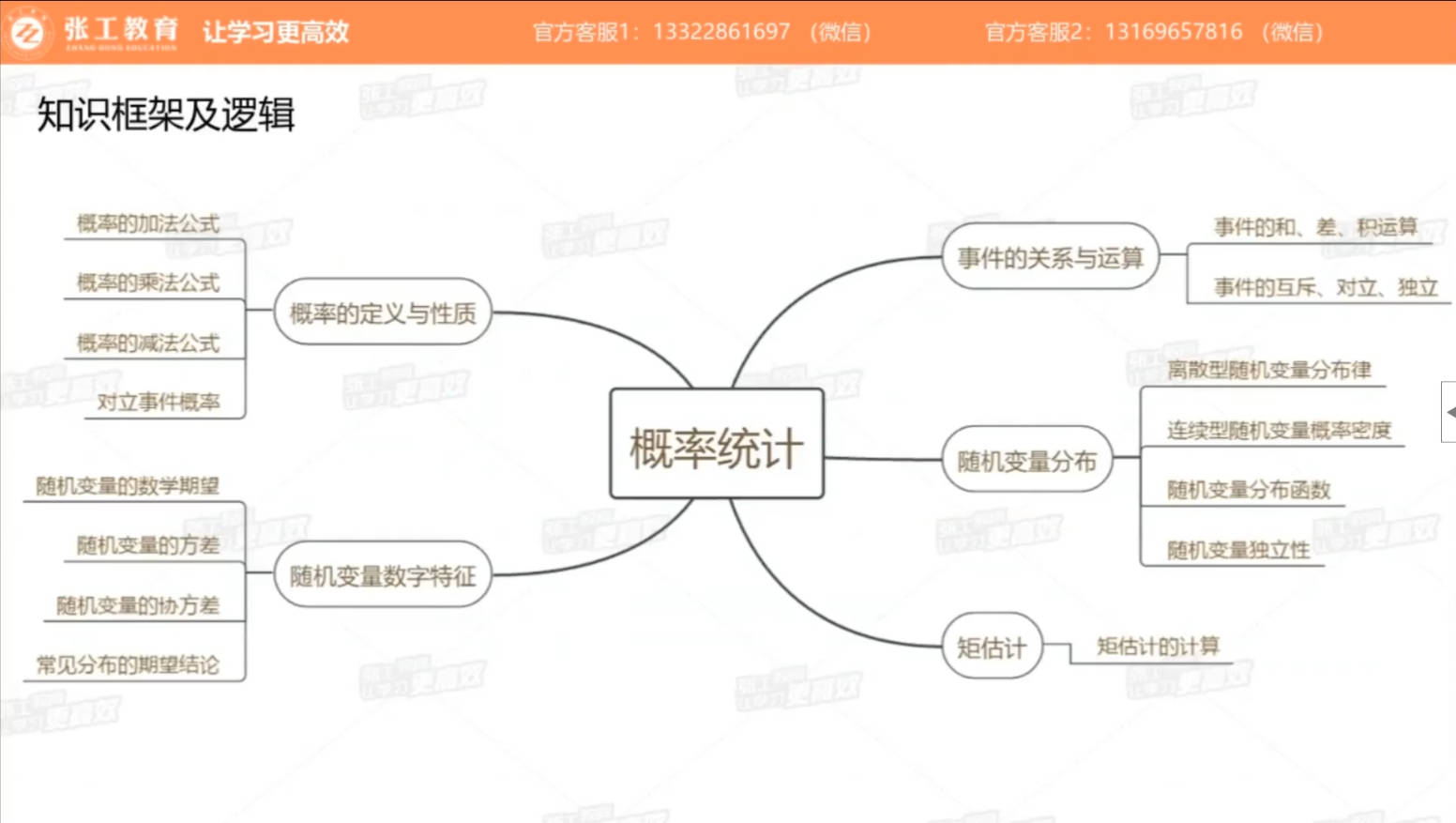
事件的关系和运算（1分）

• 事件的运算：和事件、积事件、对立事件、差事件
• 事件的关系：互斥、对立、独立
  • 对立一定互斥
  • 独立没有图形直观，不要画图
• 事件的与运算律（长杠变短杠，开口变方向）
  • 并的补=补的交
  • 交的补=补的并
• 概率的性质（必考1分）
  • 重点：互斥和、一般和、对立减、减法、乘法、独立乘
• 条件概率（条件概率做分母，乘积概率做分子）
• 古典概率模型（性价比很低、只考过两次 ）

考试快速做题指南

• 独立事件的补也是相互独立的
• 最爱：互斥的和、独立的积
• 次爱：独立的和+长短杠=>独立的积

分布函数（列）、概率密度函数（0.8分）

• 分布函数的概念
• 分布函数的性质
  • 任意区间取值概率
  • 右连续性
  • 单调不减性
  • 有界性
• 离散型随机变量及其分布律
• 连续型随机变量及其概率密度函数
• 连续型随机变量及其概率密度函数的性质
• 概率密度函数$f(x)$与分布函数$F(x)$的关系
• 常见分布：二项分布、几何分布
• 常见分布：泊松分布、均匀分布
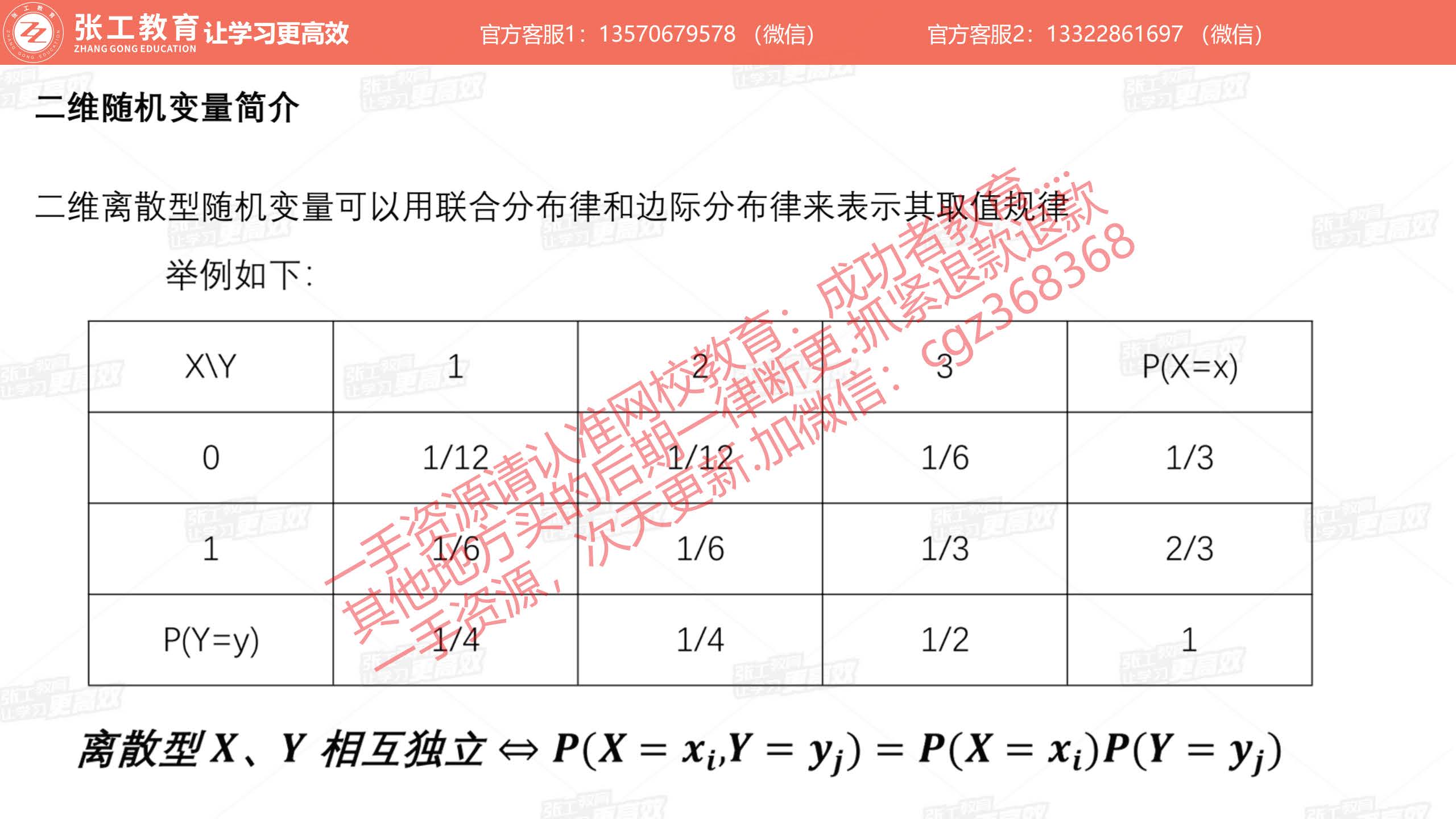
• 二维随机变量简介：二维离散型随机变量
• 二维随机变量简介：二维连续型随机变量
• 常见分布(仅学习二项分布就行了)
  • 二项分布
  • 几何分布
  • 泊松分布
  • 均匀分布
• 二维离散型随机变量
  • 联合分布律
  • 边际分布律

考试快速做题指南

• 已知泊松分布$X\sim P(\lambda )$，则 $EX=DX=\lambda$
• 均匀分布的概率密度函数为定义域上的常数：
  • 一维：$f(x)=\frac{1}{b-a}x\in [a,b]$
  • 二维：$f(x,y)=\frac{1}{\mathrm{面}\mathrm{积}}x,y\in \mathrm{面}\mathrm{积}$

数学期望和方差（0.8分）

• 数学期望的计算

  • 离散型随机变量的数学期望
  • 连续型随机变量的数学期望
  • 连续型随机变量的函数的数学期望
  • 二维随机变量的函数的数学期望
  • 常见分布的数学期望
    • 二项分布$np$
    • 泊松分布$\lambda$
    • 均匀分布$\frac{a+b}{2}$
    • 指数分布$\frac{1}{\lambda }$ 或者 $\theta$
    • 正态分布$\mu$

• 方差的定义: X偏离中心的平方的平均值

• 方差的计算公式: $D(X)=E(X^2)-(EX{)}^2=\mathrm{平}\mathrm{方}\mathrm{期}\mathrm{望}-\mathrm{期}\mathrm{望}\mathrm{平}\mathrm{方}$

• 期望和方差的性质（6个）

• 随机变量的数字特征

  • 协方差
  • 相关系数
  • 和（差）的方差

考试快速做题指南

• 常见分布的数学期望要记住，考试遇见可以秒杀拿分。如果记不住只能用公式推导了。
• X、Y相互对立=>X、Y不相关，反过来则无法得出

正态分布（0.2分）

• 正态分布的性质（6个）
• 正态分布密度图像关于$x=\mu$期望对称
• 三大分布与正态总体抽样分布：卡方分布、T分布、F分布
  • 仅记住大概结构就行了

考试快速做题指南

• 上考场前死记公式
• 设$X_1,X_2,...,X_n$来自$N(\mu ,{\sigma }^2)$,则$\bar{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$, $\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$, $\frac{\sqrt{n}(\bar{X}-\mu )}{S}\sim t(n-1)$

参数估计（0.4分）

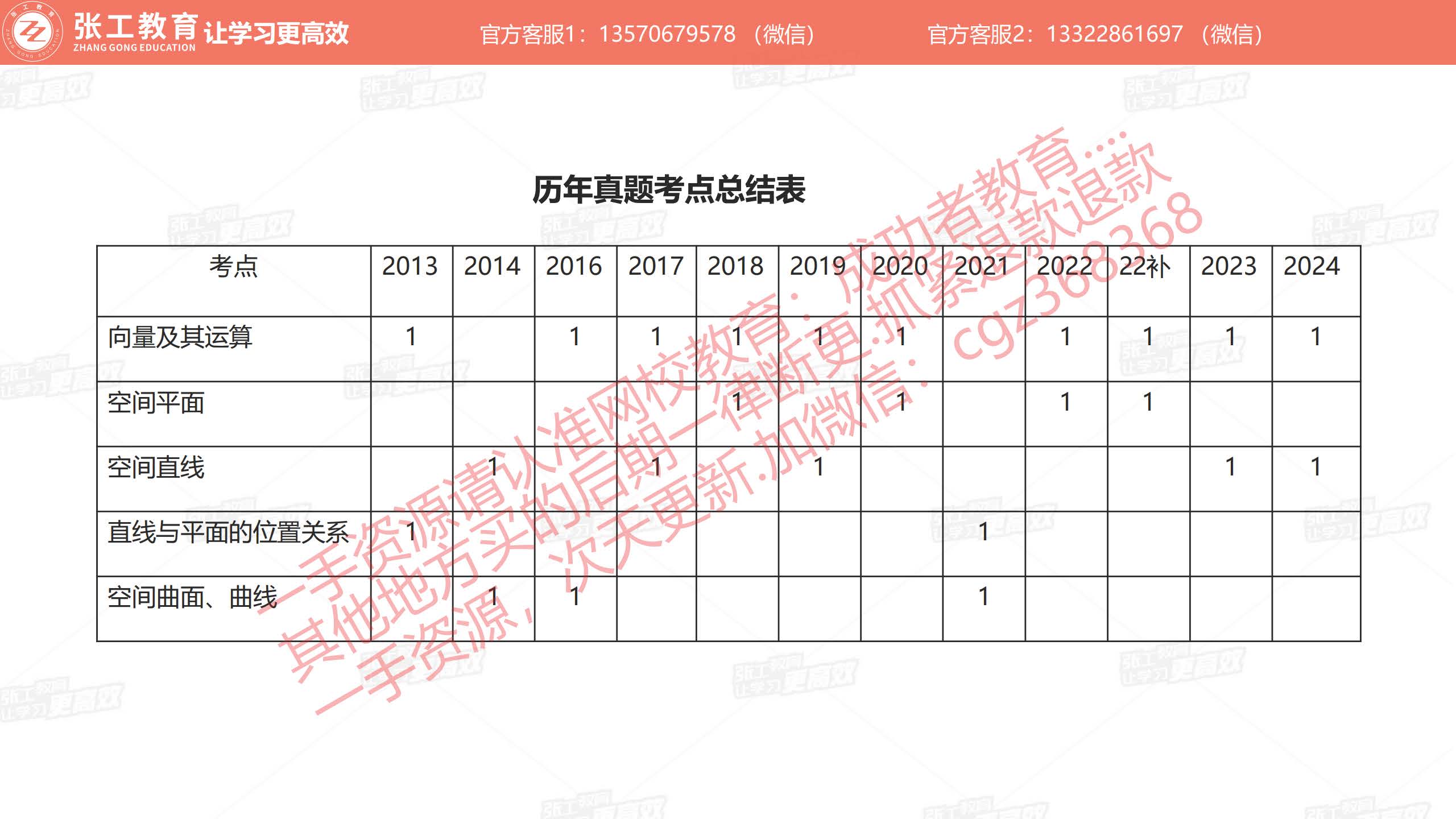
• 矩估计

考试快速做题指南

上档次考点，但很容易：只要让算矩估计，直接套公式即可$\bar{X}=E(X)$

• $\bar{X}$ 代表样本均值
• $E(X)$ 代表数学期望